An Incomplete Medical Physics Review

Basic atomic and nuclear physics

$E = \gamma m c^2$ where $\gamma = \dfrac{1}{\sqrt{1-\beta^2}}$ where $\beta = v/c$
If particle speed is much less than speed of light, $v << c$, it is not relativistic and $\gamma = 1$

Wave-particle duality:
$c = \lambda \nu$
$E = h \nu = hc / \lambda$
$E(keV) = 1.24 / \lambda(nm)$
where $E$ is energy, $\nu$ is frequency, $\lambda$ is wavelength, and $c$=3x10⁸ m/s is the speed of light.
$h$ = planck's constant = 6.626e-34 J · s = 4.136e-18 keV · s

Particle	Charge	Mass Energy (MeV)
Alpha	+2	3727
Proton	+1	938
Electron	-1	0.511
Positron	+1	0.511
Neutron	0	940

1 amu = 931.5 MeV = 1/12 mass of ¹²C
1 mole = 6.02214076 × 10²³ atoms, exactly (Avogadro's number).
Legacy definition: 12 g of ²C atoms = 1 mole.

Electrons/positrons are ~ 1,800x less massive than protons and neutrons.

Electronvolt (eV): kinetic energy of an electron gained by acceleration through a potential difference of 1 volt.
1 eV equal to 1.602176634×10⁻¹⁹ J

Ionizing radiation: has sufficient energy to remove bound electrons. Energy threshold depends on matter type, nominally ~ 11 eV
Ca: 6.1 eV, glucose: 8.8 eV, water: 11.2 eV
Average energy expended per ion pair: W ~ 34 eV (used in exposure to dose conversion)

Electrons and positrons emitted from radioactive nuclei are called beta-minus (negatrons) and beta-plus particles.
Electron shells: K (1), L (2), M (3), N (4), ... max electrons: 2n²
K shell has highest binding E. Binding E increases with Z (E_H = 10.1 eV, E_W = 58.5 keV).

Characteristic x-ray: radiation emitted from electrons transitioning from an outer to an inner shell.
Energy of x-ray depends on the atom and is the difference between the binding energies of the two shells.
K-characteristic x-ray: vacancy in the K-shell. L → K is $K_\alpha$ transition (alpha for adjacent shells).
Fluorescent yield: probability that transition will result in characteristic x-ray.
Auger electron: released energy from transition is transferred to orbital electron. Probability is 1 - fluorescent yield. Ejected electron is imparted with the difference in binding energy of the downward transitioning electron, minus its own binding energy.
Auger emission dominates for low Z elements and for outer shell transitions for high Z. For Z < 10, K-shell fluorescent yield < 1%, Z = 20 (Ca) ~ 15%, Z = 53 (I) ~ 65%, Z > 60 ~ 80%.
Molybdenum (₄₂Mo) and Ruthenium (₄₄Ru) are useful for producing characteristic x-rays of a desirable energy (~20 keV) in mammography.

Nuclides

Atomic nucleus contains protons and neutrons held together by strong force mediated by gluons. Discovered in gold foil experiment by Rutherford. Radius in the range of 1-6 fm (atomic radius ~50-150 pm)

Isotope: same number of protons, Z -- e.g. I-131 and I-125
Isobar: same atomic mass number A -- e.g. Mo-99 and Tc-99
Isotone: same number of neutrons (A-Z) -- e.g. I-131 and Xe-132
Isomer: same Z,A, different energy states -- e.g. Tc-99m

Most nuclides have an even number of protons and neutrons. Some have even/odd or odd/even and provide NMR signals. Only H, Li, B, N, and Ta have stable isotopes with odd/odd.

X-rays: photons emitted from atoms or electrons (excitation, characteristic, bremsstrahlung).
Gamma rays: photons of nuclear origin -- radiation emitted when nucleus drops from an excited state to a lower more stable energy state. They are also often more energetic.

Interactions of photon and particle radiation with matter

Collisional: excitation and ionization -- interactions with orbital electrons.
Excitation and ionization probabilities are usually equal around 40 eV
Average energy deposited per ion pair (W) in air is 34 eV and in soft tissue is 22 eV.
Delta rays: secondary ionization from sufficiently energetic ejected electrons from an initial ionization.
Specific ionization $SI \propto Q^2/v^2$: average number of ion pairs produced per unit length of charged particle's path (IP/mm). Depends on charge $Q$ and velocity $v$.

Path length (distance traveled) ≥ range of charged particle (start to end point, depth of penetration)
Linear energy transfer (LET): average energy deposited locally in the absorber per unit path length.
$LET \propto Q^2/E_k$ → lower kinetic energy particles deposit more local energy per path length, as do higher charged particles.
Local energy deposition density (has radiobiological significance) -- more damage with higher LET.
Diagnostic x-rays ~ 3 keV/μm vs alpha particle 5-MeV ~ 100 keV/μm.

Scattering: elastic (no energy change) or inelastic (less kinetic energy after collision)

Radiative - bremsstrahlung: charged particle path deflected, loss of kinetic energy, emission of photon (conserve energy). Photon energy can be any value up to the kinetic energy of deflected particle
Probability proportional to Z²/m² → high-Z materials create a lot more radiation, high mass charged particles don't produce much bremsstrahlung (electrons lots of bremss, protons, little bremss).
Used in x-ray tubes to generate x-rays from electrons incident on a high-Z material (e..g Tungsten, Z=74).
Bremsstrahlung energy efficiency (output x-rays from input electron energy) ~ $9 \times 10^{-10} Z E$ where Z is material atomic number and E is the accelerating energy (volts)

Positron annihilation: at the end of its (short) range, a positron annihilates with an electron and produces two 0.511 MeV photons in opposite directions (used in Positron Emission Tomography).

X-ray and gamma-ray interactions

Rayleigh scattering: photon interacts with total atom. EM field creates in-phase oscillations of electron cloud, which radiates energy. Low energy photons, no ionization. Same energy photon emitted, different direction (greater angle for lower energies).
Less than 5% of diagnostic x-ray interactions above 70 keV (~10% at 30 keV).

Photoelectric effect: Incident photon energy is transferred to electron, which is ejected. Kinetic energy of electron is equal to incident photon energy minus the binding energy: $E_{e} = E_{p} - E_{b}$.
Ejected electron most likely to be one with binding energy close to, but less than, the photon energy.
Electron cascade follows as vacancies are filled from lower binding shells → characteristic x-rays or Auger electrons. Lower Z, fewer x-rays (not many in soft tissue).
Photons on certain high-Z materials can interact with valence electrons (low work function), electrons released, but no cascade (e.g. PMT).
Probability per unit mass of a photoelectric interaction is proportional to $Z^3/E^3$. High Z materials (e.g. ₅₃I) undergo more photoelectric interactions → useful for image contrast. Lower energies → higher contrast images.
Dominates for lower energy photons in higher Z materials.
No scattered photons to degrade images.
Absorption edges: probability above the edge is much greater than slightly below edge, the energy of which corresponds to binding energy of a shell. The energy of each edge increases with increasing Z.

Compton scattering: Inelastic/nonclassical scattering. Most common interaction in soft tissue for most medical physics modalities (26 keV to 30 MeV). Photons and valence electrons, electron is ejected and photon is scattered, and both share the incident energy.
Incident photon energy equals sum of scattered photon and electron kinetic energy: $E_o = E_{sc} + E_{e-}$

The change in the photon wavelength after scattering, depends on the scattering angle: $$\lambda' - \lambda = \frac{h}{m_e c}(1-\cos{\theta})$$ where $\lambda$ is the initial wavelength, $\lambda'$ is the wavelength after scattering, $h$ is the Planck constant, $m_e$ is the electron rest mass, $c$ is the speed of light, and $\theta$ is the scattering angle.

The scattered energy can similarly calculated as
$$E_{sc} = \frac{E_o}{1+(E_o/m_e c^2)(1-\cos{\theta})}$$ where $E_{o}$ is the original photon energy, $E_{sc}$ is the scattered photon energy, $m_e c^2$ is the electron mass energy (511 keV), and $\theta$ is the scattering angle.

The differential cross section of Compton scattering (and Thomson at lower energies) is given by the Klein-Nishina formula. This formula describes the distribution of scattering angles at a given photon energy.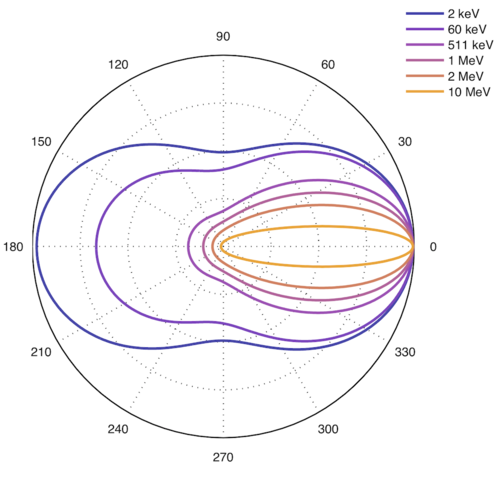

$$\begin{eqnarray} {\frac {d\sigma }{d\Omega }}={\frac {1}{2}}\alpha ^{2}r_{c}^{2}P(E_{\gamma },\theta )^{2} \times   \nonumber  \\ [P(E_{\gamma },\theta )+P(E_{\gamma },\theta )^{-1}-\sin ^{2}(\theta )]   \nonumber \end{eqnarray}$$

where $P(E_{\gamma },\theta )$ is the ratio of energies, $E_{sc}/E_{o}$, $\alpha$ is the fine structure constant (~1/137), and $r_c = \hbar / m_e c$ is the reduced Compton wave length of the electron.

Higher energy → more forward scattering.

Max E to electron is for 180-deg backscatter, max angle is 90 deg.
Max E to photon is 511 keV at 90 deg, and 255 keV at 180-deg., any angle possible.
Probability (cross section) depends on electron density $N_A\,Z/A$ (also ~density) and energy, but independent of Z (electrons/g fairly constant in tissue). Hydrogen has high electron density, more likely to Compton scatter.
Diagnostic energies (15-150 keV) → most energy to scattered photon → degrades image quality.

Pair production: Photons with energy above 1.02 MeV (2 x 0.511 MeV, rest mass of e- & e+) interacting with the electric field of a nucleus can be transformed into an electron positron pair. Excess energy above the combined rest masses becomes kinetic energy, which is then lost via excitation and ionization.
Probability of pair production $\propto Z\,ln(E)$
Sort of the opposite of electron-positron annihilation. Does not dominate until energies around 20-30 MeV.
Angle between the particles is proportional to 1/E (conservation of momentum).

to the top

Charged Particle Interactions

Charged particles generally interact through the Coulomb force: $F = k q_1 q_2/r^2$

Charged particles are directly ionizing by collisions (photons are indirect).

Charged particles lose kinetic energy gradually, in a friction-like process.
Typically use the continuous slowing down approximation (CSDA).

Soft collisions: occur when impact parameter is much larger than the atomic radius.
Coulomb force "sees" whole atom, excites or ionizes by ejecting valence electron. Small energy transfer

Hard collisions: occur when impact parameter close to the atomic radius
Column force between particle and single electron, ejects it as high energy delta ray
Higher energy transfer but less probable.
Inner electrons ejected result in characteristic x-ray or Auger electrons.

Nuclear field interactions: occur when impact parameter is much less than atomic radius
Elastic (97-98%): deflection, no energy transfer, lots of scatter, $\propto Z^2$
Inelastic (2-3%): can result in bremsstrahlung x-rays, $\propto Z^2/m^2$ (only electrons affected)

Nuclear interactions: occur with heavy charged particles. Need ~ 100 MeV.
Loss of fluence, results in local and non-local (neutron) fragments. Can also create short-lived positron-emitting isotopes (¹¹C, ¹³N, and ¹⁵O).

Stopping power: rate of energy loss per unit path length for a given particle in a given medium (includes collisional and radiative)
Mass stopping power depends on particle energy, charge, mass, and medium (ionization energy, atomic number, atomic mass).

$(dT/dx)_c \propto N_A Z / A$
$(dT/dx)_r \propto N_A Z^2 / A$

Range: Approximate by integrating stopping power over energy $R_{CSDA} = \int_0^{T_0} \left(\frac{dT}{\rho dx}\right)^{-1} dT$

Range variation occurs because of multiple scattering (lateral spatial spread) and range straggling (energy spread after slightly different path lengths and number of collisions). Much higher effect for electrons than heavier charged particles.

Relative ranges for same initial velocity: $R_1 / R_2 = (M_1/M_2) \cdot (Z_2/Z_1)$

Electrons

Energy loss of high energy electrons is mostly ionization/excitation in low Z and bremsstrahlung in high Z.
Rate of energy loss from bremss is $\propto E$ and $\propto Z^2$, while collision is $\propto Z$
Collision stopping power dominates at low energy and radiative at high energy.

Electrons moving faster than the phase velocity of photons in a medium will emit a cone of electromagnetic radiation called Cherenkov radiation. Radiation is mostly in the ultraviolet range, with some visible blue-violet wavelengths.

Protons

Protons and other heavy charged particles experience a Bragg peak, wherein the majority of dose is deposited at the end of range. (The peak is sharper for higher mass particles, e.g. ¹²C beam)

The range of 250 MeV protons in water ~ 40 cm (deep prostate), while 70 MeV ~ 4 cm (eye treatments)

$dE/dx \propto Z z^2 / \beta^2$ (approximately) where $Z$ is effective atomic number of material, $z$ is charge of particle, and $\beta$ is speed of particle relative to speed of light.

Neutron Interactions

Uncharged, can only interact with atomic nuclei, often exciting and ionizing. Mostly interact with hydrogen in tissue (water). Neutron capture (by nuclei) releases much energy (2-7 MeV) because of large neutron binding energy. Neutrons can be reemitted or create (usually unstable) isotopes.

Similar PDD as photons. Higher LET.

Interactions described by cross sections (analogous to mass attenuation coefficients for photons). Units of barns = 10^-24 cm².

Macroscopic cross section $\Sigma = \sigma N$ where $\sigma$ is microscopic cross section and $N$ is atomic density. Units of cm^-1. Depends strongly on neutron energy, material, and interaction type

• Scattering (fast neutrons)
  • Elastic (n,n)
  • Inelastic (n,n'), (n,nγ): 1H(n,n')1H
• Absorption
  • Capture (thermal neutrons)
    • EM (n,γ): 1H(n,γ)2H
    • Charged (n,p),(n,α),(n,d): 14N(n,p)14O
    • Neutrons (n,2n),(n,2n),(n,3n)...
  • Fission (n,fission)

Intensity: flux = fluence rate = $\phi = n \times v$ = neutron density times speed.
Attenuation: $\phi = e^{\sigma N x} = e^{\Sigma x}$
$\lambda = 1/\Sigma$ = ~ 1 cm for thermal (~ eV), and tens of cm for fast.

Photoneutron production (γ, n) in ≥ 10 MV beams.

Hydrogen best material to slow down neutrons (has 1 nuclide, interacts well with 1 neutron)
Energy transferred: $\Delta E_{max} = \dfrac{4A}{(1+A)^2} E_n$

Boron-10: Large absorption cross section $^{10}\text{B}(n,\alpha)^7 \text{Li}$, Q = 2.79 MeV
σ = 3843 barns at 0025 eV.
Used for detection and suppression.

Radioactivity

Decay pathways: Many isotopes are unstable because they have high mass, the neutron to proton ratio (N/Z) is too small or too large, or the nucleus is in an excited state.

Graph of isotopes by type of nuclear decay.
Wikimedia Commons

Alpha decayAlpha particle (2n2p) emitted. Atomic number Z is reduced by 2, mass A reduced by 4. Typically occurs for atoms with A > 150. Often followed by photon emission. Alpha particles energies typically between 2 to 10 MeV (discrete energies). Little penetration (< 100 μ in tissue) but high energy transfer.

E.g., ${}^{223}_{88}Ra \rightarrow {}^{219}_{86}Rn$, used in treatment for cancer metastasis.

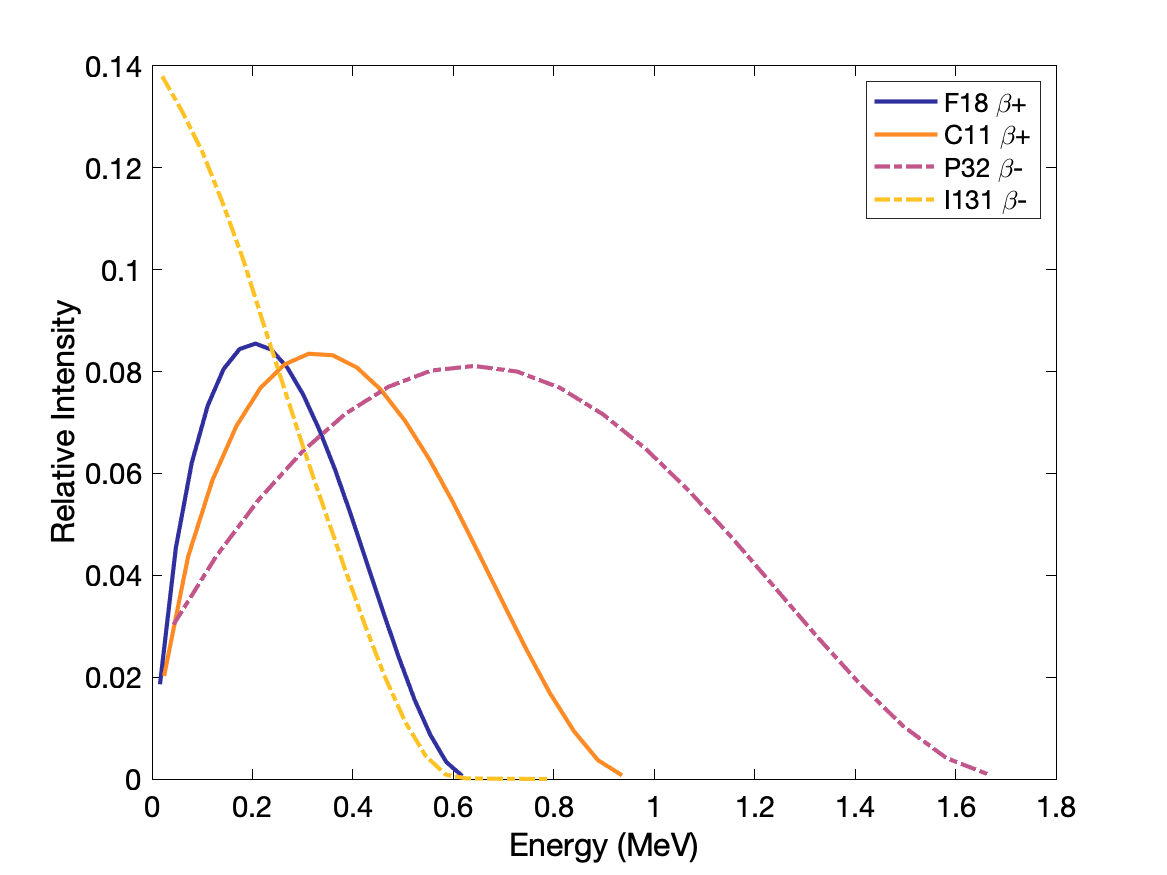
Beta plus (positron) decay: proton becomes neutron, positron is emitted. Atomic number Z decreases by 1, mass stays same. Parent atom must have mass greater than daughter atom by at least the masses of positron and orbital electron (1.022 MeV).  Proton rich nuclei.
E.g., ${}^{18}_{ 9}F \rightarrow {}^{18}_{ 8}O $, used in cancer detection and staging.

$p  \rightarrow n + \beta^+ + \nu$

Beta minus decay: neutron becomes proton and electron is emitted. Atomic number Z increases by 1, mass stays same. Average electron energy is ~ 1/3 E_max (rest goes to antineutrino).  Neutron rich nuclei. 
E.g., ${}^{131}_{53}I \rightarrow {}^{131}_{54}Xe$

$n  \rightarrow p + \beta^- + \nu$

Electron capture: proton captures an electron (usu. K- or L-shell) to become a neutron, with x-rays and Auger electrons emitted. Atomic number decreases by 1, mass stays same. Proton rich nuclei.
E.g., ${}^{201}_{81}Tl \rightarrow {}^{201}_{80}Hg$, used in myocardial perfusion studies.

$p + e^-  \rightarrow n + \nu$

Isomeric transition: Excited nucleus releases gamma rays or ejects an orbital electron as it de-excites. No change in Z or A.
E.g. ${}^{99m}_{43}Tc \rightarrow {}^{99}_{43}Tc$, used in many nuclear medicine applications, emits 140 keV gammas.
Internal conversion occurs when the excitation energy of nucleus goes to ejecting an orbital electron with distinct energy. The vacancy is filled with cascade of characteristic x-rays and auger electrons (as above).

Spontaneous fission: Very heavy element breaks into smaller, nearly equal in mass, nuclei. Much less common than alpha-decay. Neutrons released.

Mass defect/deficit: difference in mass of an atom vs the unbound constituent particles (binding energy).
$m = Z m_{p} + (A-Z) m_{n} - \frac{E_{B}}{c^{2}}$ where $Z$ is number of protons, $A$ is atomic mass (A-Z is neutrons), $m_p$ is mass of proton, $m_n$ is mass of neutron, and $E_B$ is the binding energy of the nucleus.
Average binding energy per nucleon, $E_B$ peaks around iron, below which fusion release energy, and above which fission releases energy (in form of photons and particles with kinetic energy).

Depending on the isotope, multiple decay modes may be possible, with the probability for each decay referred to as the "branching fraction" or "branching ratio". E.g., Na-22 decays by positron emission for about 90% of the decays, and by electron capture 10% of the time.

Increasing A  ↓	α
		β+, E.C.	Parent, Isomeric	β-
	Increasing Z→

Radioactive Decay

The activity, or rate of change in the number of radioactive atoms, is proportional to the current number of atoms. The proportionality is determined by the isotope's half-life, $T_{1/2}$ or the decay constant $\lambda = ln(2)/T_{1/2}$
$A = -dN/dt = \lambda N$
Integrate to get number of radioactive atoms (or activity) at time $t$ based on original number $N_0$ or original activity $A_0$
$N(t) = N_0 e^{-\lambda t}$ or $A(t) = A_0e^{-\lambda t}$

Radioactivity SI unit is Becquerel (Bq) equal to one disintegration per second. Unit still commonly used (in USA) is the Curie, where Cu = 3.7 x 10¹⁰ Bq.
Typical amounts injected for nuclear medicine imaging are in the range of ~10 mCi = 370 MBq.

Mean life is $1/\lambda = T_{1/2} / \text{ln}(2)$

Cumulated activity from initial activity: $\tilde{A} = A \times T_{mean} = A \times T_{1/2} \,/\, \text{ln}(2)$
Aka "Time integrated" (uses the $\text{ln}(2)$ factor)

Remaining fraction: $f = (0.5)^n$ where $n$ is the number of half-lives elapsed 

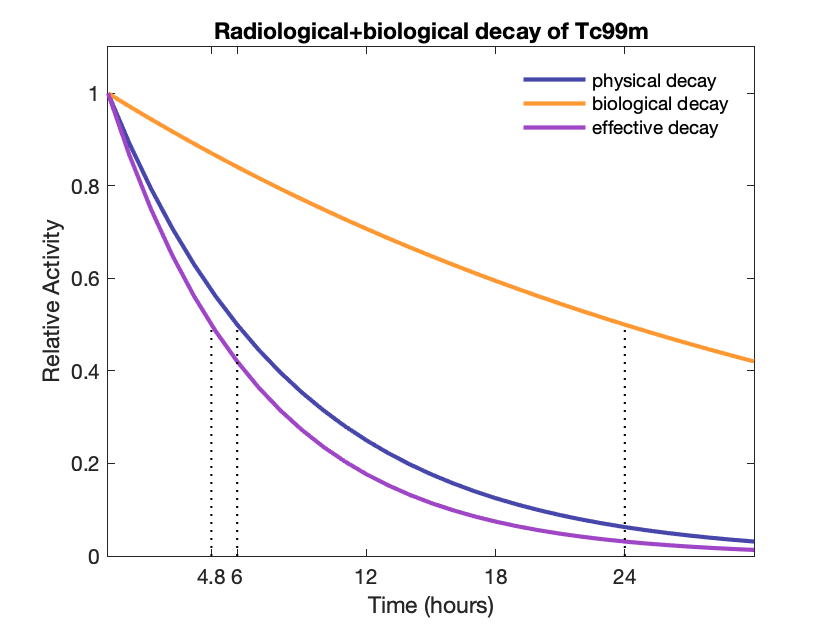
Effective half-life (physical + biological): $T_e = \frac{T_p \cdot T_b}{T_p + T_b} = 1 / (1/T_p + 1/T_b)$
Effective decay constant: $\lambda_e = \lambda_p + \lambda_b$

Transient and Secular equilibrium
Often a radioactive isotope will decay into another radioactive isotope. It is useful to know the relative concentrations of each.
To find the daughter activity, one can use the Bateman equation:
$${\displaystyle A_{d}=A_{P}(0){\frac {\lambda _{d}}{\lambda _{d}-\lambda _{P}}}\times (e^{-\lambda _{P}t}-e^{-\lambda _{d}t})\times BR+A_{d}(0)e^{-\lambda _{d}t},}$$ where $A_P$ and $A_d$ are the parents and daughter activities, $T_P$ and $T_d$ are the corresponding half-lives, and $\lambda_P$ and $\lambda_d$ are the corresponding decay constants. BR is the branching ratio.
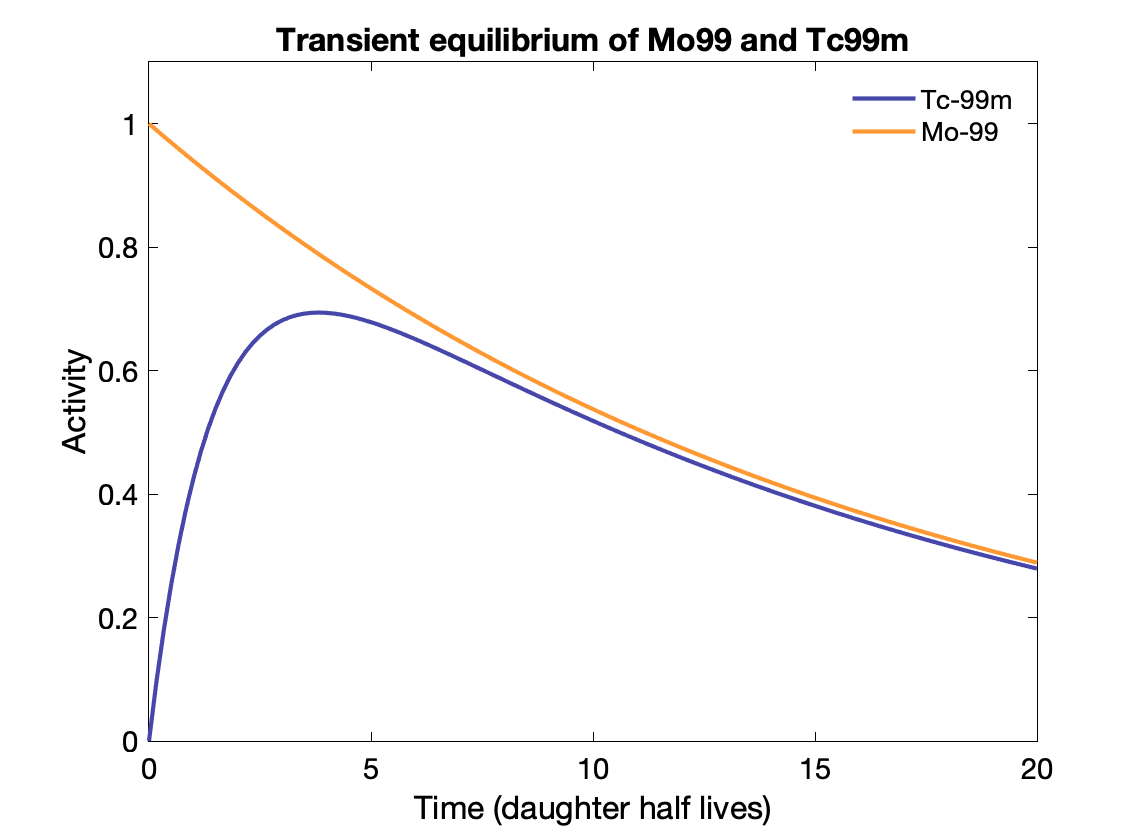
Transient equilibrium: Daughter half-life is shorter, and daughter activity depends on parent activity, but is not the same:
${\displaystyle {\frac {A_{d}}{A_{P}}}={\frac {T_{P}}{T_{P}-T_{d}}}\times BR.}$
Time to transient equilibrium: $t = \frac{\text{ln}(\lambda_d / \lambda_p)}{\lambda_d - \lambda_p}$

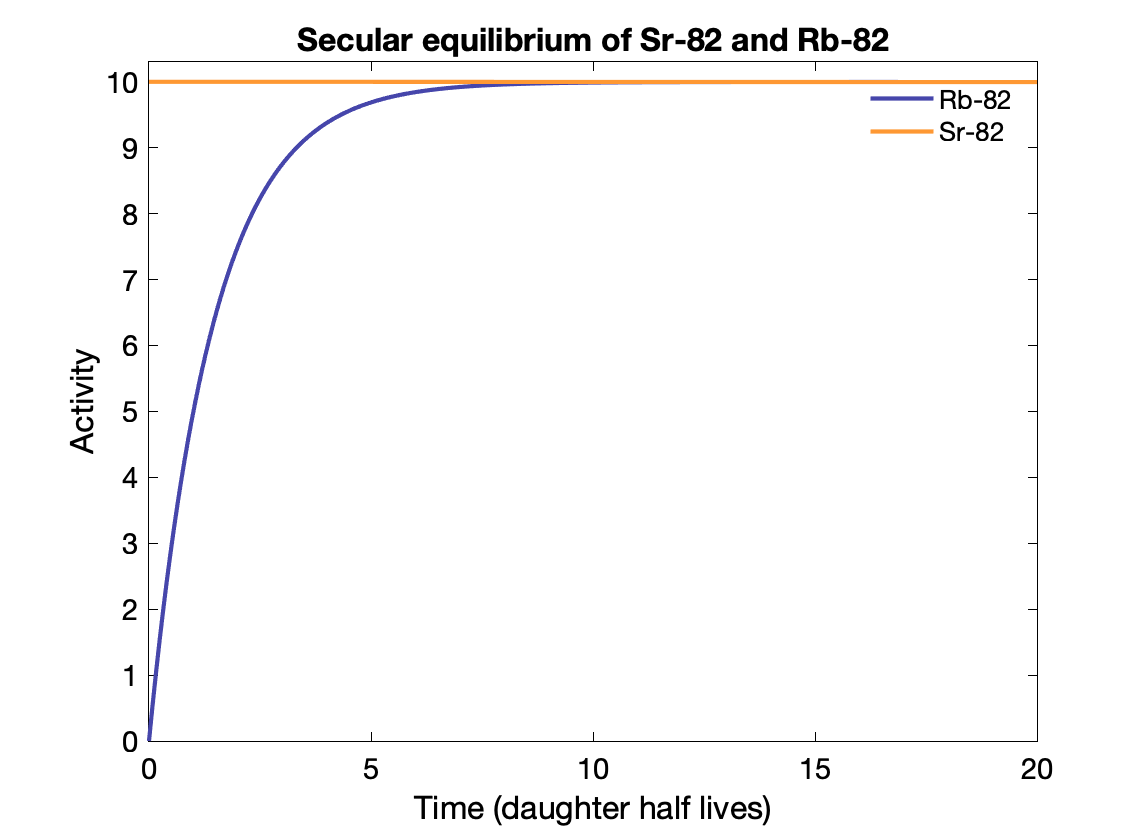
Secular equilibrium happens where the parent half-life is much longer (> 100x) than the daughter's. After 5-6 half-lives, the activity of the parent and daughter are the same if the BR = 1. The daughter activity is produced at the same rate it decays?
E.g., Sr-82 → Rb-82 (25.5d vs 75s).

Note that the Mo-99 only decays to Tc-99m with a branching fraction of 88%, otherwise Tc-99m activity would exceed the parent activity.

Specific activity
Activity per unit mass: $a = \frac{\lambda N_A}{m} = \frac{ln(2) N_A}{T_{1/2} \times m}$ (in Bq/g) where N_A is the Avogadro constant.

Carrier-free specific activity (CFSA): $A \text{(Bq/g)} = \frac{ln(2) N_A}{T_{1/2}}$
If other isotopes of the same element are also present in the sample, is it not carrier free and the specific activity is lower.

High specific activity is usually desirable because then a very small amount of a compound can be administered, thus creating no pharmacologic effect.  

Sources of radioactive material

Uses of radioactive material: Co-60 teletherapy, brachytherapy seeds, therapeutic nuclear medicine, and diagnostic nuclear medicine

Cyclotron produced
High energy charged ions are used to bombard stable nuclei and convert them into radioactive isotopes. Cyclotrons use magnetic and electric fields to accelerate ions in a circle, building up speed until and increasing in radius until they are removed from the path and aimed at a particular target. The energy of the ion depends on the particle, the diameter of the system (electromagnetic "dees") and the electromagnetic field strength.
Collision with the target nuclei results in occasional nuclear reactions, resulting in unstable (excited) atoms that decay.
Common example: ${}^{18}O(p,n){}^{18}F$ where a proton interacts with an ${}^{18}O$ nucleus to produce a ${}^{18}F$ atom that decays by positron emission with a 109.7 minute half-life. Note: ${}^{18}O$ occurs naturally but with very low abundance. The target sample is ${}^{18}O$ enriched water.
Most cyclotron-produced radionuclides are neutron poor and thus decay by positron emission or electron capture.

Nuclear reactor produced: Fission and Reactor

Fission produced High specific activity (easy to chemically separate). Mo-99, I-131, Xe-133.

Neutron activation produced Stable nuclei capture neutrons from the reactor (from fission of uranium). Slow (thermal) neutrons typically have a (n,γ) reaction, but (n,p) and (n,α) are also possible. These neutron rich isotopes typically decay by beta-minus emission.
E.g., ${}^{31}P(n,\gamma){}^{32}P$
Same Z, difficult to separate radioactive from stable atoms → low specific activity.

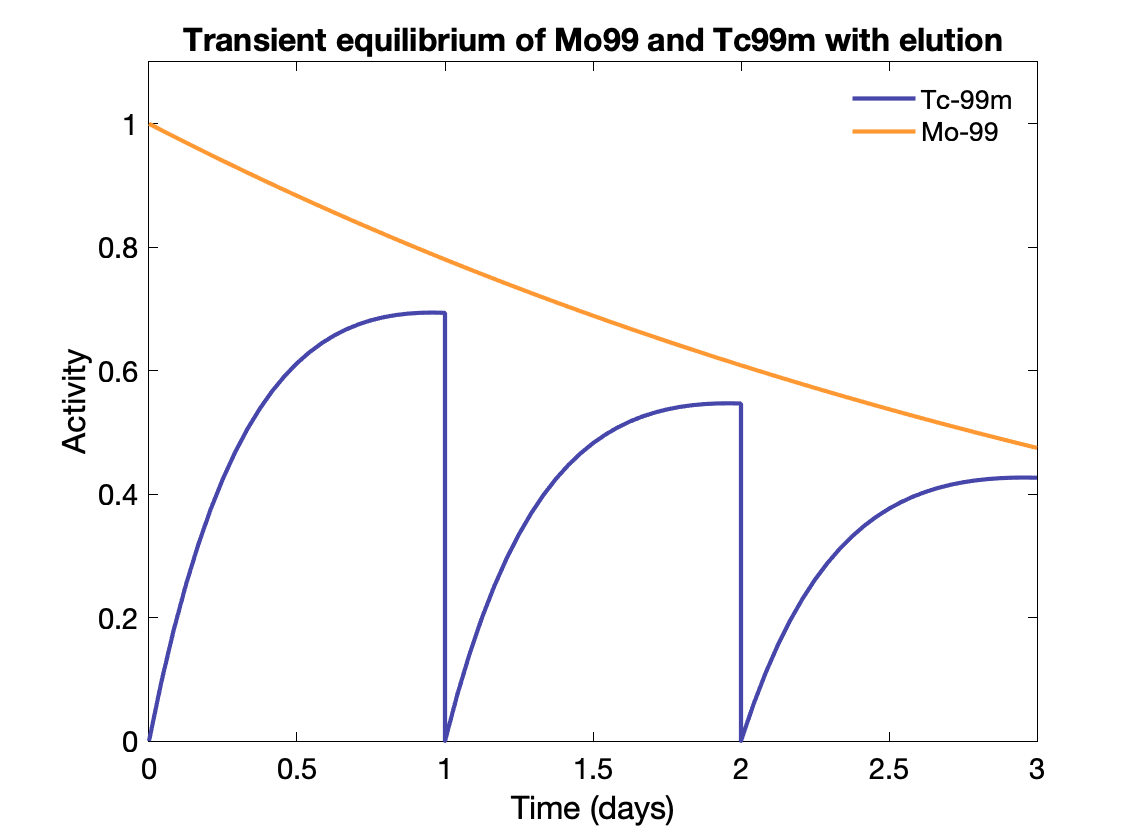
Generators Parent with long half-life used to generate isotopes with usable half-lives. E.g., Mo-99 (67 h) to Tc-99m (6 h). Tc-99m collected from the generator periodically for use.
Separation is done using a porous column of resin (Al2O3), absorbs the parent Mo-99 but lets the daughter Tc-99m pass through when eluted with saline. Product is $Na^+({}^{99m}TcO_4^-)$, sodium pertechnetate.
Generator starts with 37 to 740 GBq (1 to 20 Ci).
Activity of daughter depends on activity of parent, rate of formation of daughter (decay rate of parent), decay rate of daughter, time since last elution, and elution efficiency (usu. 80-90%).
For Molybdenum, maximum elution at 23 h (transient equilibrium achieved).

Saturation activity: maximum amount of activity that can be produced (equilibrium reached between production and decay)

$A(t) = \Sigma \cdot \Phi \cdot (1-e^{-\lambda\,t})$ where activity over time is activation rate (cross section $\Sigma$ × flux density $\Phi$) minus decay rate, and at t→∞  saturation is reached: $A_s =  \Sigma \cdot \Phi$

$f = 1 - (1/2)^n$ where $f$ is the fraction of saturation and $n$ is the number of half-lives

to the top

Radioactive material uses and safety

PET imaging isotopes

Radio nuclide	Physical half-life (min)	Positron energy (MeV)	Range in soft tissue (mm)	Production method
C-11	20	0.96	4.1	Cyclotron
N-13	10	1.19	5.4	Cyclotron
O-15	2	1.73	7.3	Cyclotron
F-18	110	0.635	2.4	Cyclotron
Ga-68	68	1.9	8.1	Generator (Ge-68)
Rb-82	1.3	3.15	15	Generator (Sr-82)

Nuclear medicine

Molybdenum: Limits on contamination of Mo-99 in Tc-99m ("Molybdenum breakthrough"). Bad because of long half-life with energetic betas and gammas that are not useful for imaging and only add to dose. Limit of 0.15 μCi of Mo-99 per mCi of Tc-99m at administration time.

Radiation generating equipment: photons, electrons and heavy particles

X-ray tubes: consist of tungsten filament as the cathode and source of electrons, tungsten (usually) target connected to copper anode, all inside a vacuum. Electrons from cathode are accelerated to the angled anode using a voltage difference. Interaction with the tungsten produces x-rays through bremsstrahlung.
Electrons are produced through thermionic emission from the heated filament
Most of the (collisional) interactions produce heat. The few (~1%) electrons deflected by the nuclei are the source of bremsstrahlung photons, along with a few characteristic x-rays, that make up the x-ray beam.
The maximum energy of the photons is the electron energy, determined from the voltage difference. The minimum energy is zero, but filtering removes most of the lower energy photons.
X-ray spectrum is determined from the target material (Z) and the kinetic energy of the electrons.
Tube current (mA) is proportional to the number of electrons per second moving from cathode to anode. Current can range from 1 mA (fluoroscopy) to 1,200 mA (projections).

Parameters: kilovoltage (kV), determining the maximum photon energy, current (mA), corresponding to the number of photons per second, and exposure time (s), affecting the total number of photons in the exposure.
Current and time are often combined (mAs) as a metric for dose and image quality.
Higher voltages ~ slightly higher tube current for same filament current.

Anode target is typically tungsten (molybdenum or ruthenium for mammography b/c of characteristic x-rays) because of high Z (74) and high melting point. Target can be stationary (dental and some mobile units) or rotating. Rotation distributes the electron beam over a larger area ($2 \pi r \Delta r$) and spreads out the heating. Rotor assembly uses induction to spin the beveled anode, and bearings can be cause of x-ray tube failure.

The angled (or beveled) anode changed the focal spot size based on the sine of the angle: Effective length = actual length x sin(θ)
The angle is typically between 7 and 20 degrees, usually around 12-15 deg. Angle affects not just spot size from also output intensity and field coverage. Smaller angle (steeper) leads to smaller focal spots (better resolution) but smaller field coverage.
Spot size measured/verified with pinhole or slit camera, star pattern, or resolution bar pattern.
Focal spot blooming (increase) can occur at high tube current and low kV (repulsion of beam).

Heel effect: reduction of beam intensity on anode side of field. Lower effect for longer source to image distance. Put cathode side over thicker parts of object. Occurs because of higher self-attenuation for photons going through more of the anode material.

Linacs: Linear accelerators are used to generate high energy photons and/or electrons for therapy.

Cyclotron/Synchrotrons: Circular accelerators are used to generate high energy heavy ions (protons, carbon, etc) for therapy.

Dosimetry concepts and units

Exposure: $X = dQ/dm$ where $dQ$ is the total charge of ion pairs produced in air when all liberated electrons in mass of air $dm$ are stopped.
Units: Roentgen R, C/kg. 1 𝑅=2.85×10^-4 (𝐶/𝑘𝑔)
Valid only for photons.

Dose: Amount of energy imparted by radiation per unit mass. Units: Gy = J/kg = 100 rad

Kerma: Kinetic energy transferred to charged particles per unit mass. Units: Gray (Gy) = J/kg = 100 rad

Equivalent dose: Dose weighted based on the biological effectiveness of the radiation, which depends on the radiation type and energy. Units: Sieverts (Sv) = J/kg = 100 rem
Photons, electrons, muons have weight of 1.
Neutrons have weights of 5 for E < 10keV, 10 for 10 < E < 2 MeV , 5 for E > 20 Protons have weight of 1.1 to 2 for E > 2 MeV Alpha particles, heavy nuclei have weight of 20

Effective dose: Dose weighted based on the biological sensitivity of the exposed tissues and organs. Units: Sieverts (Sv) = J/kg = 100 rem

Beam descriptors

• Fluence: number of rays per unit area, $\Phi = \frac{dN}{dA}$
• Flux density: fluence per unit time, $\phi = d\Phi/dt = \frac{d}{dt}(\frac{dN}{dA})$
• Energy fluence: energy per unit area, $\Psi = \frac{dE}{dA} = \frac{dN}{dA} E = \Phi E$
• Energy flux density: energy fluence per unit time, $\psi = d\Psi/dt = \frac{d}{dt}(\frac{dE}{dA})$

Kerma: kinetic energy released per unit mass $K = \frac{dE_{tr}}{dm} = \Psi(\frac{\mu_{tr}}{\rho}) =\Psi(\frac{\mu_{en}}{\rho}) / (1-g) $ in units of Gy.
$\Psi$ is photon energy fluence (MeV/cm²), $\mu/\rho$s are mass energy transfer and absorption coefficients (usually in  cm²/g), and $g$ is average fraction of electron energy lost to radiative processes.
$\mu/\rho$s depend on Z of target and energy of photons (lookup tables).

Kerma includes both collision and radiative energy $K = K^{col} + K^{rad} = \Psi(\frac{\mu_{en}}{\rho}) + \Psi(\frac{\mu_{en}}{\rho}) (\frac{g}{1-g})$

Exposure & Kerma: $X = (K^{col})_{air} \cdot (\frac{e}{\bar{W}})  = \Psi(\frac{\mu_{en}}{\rho})(\frac{e}{\bar{W}}) $ where $e$ is electronic charge (1.602 × 10^−19 C) and $W=33.97$ eV/ion pair is the energy required to produce an ion pair in dry air.  $\bar{W}/e = 33.97$ J/C

Kerma is highest on entry of photons in a medium. Dose takes some depth to build up. Dose increases above kerma, then both decrease at the same rate (transient equilibrium). Caused by electron range and forward motion.  Ratio varies with photon energy but not medium. Total area under kerma and dose curves vs depth must be same.

$D_{air} = \Psi (\frac{\mu_{en}}{\rho}) = (K^{col})_{air}  = X \cdot \frac{\bar{W}}{e}$ → conversion factor of R to cGy in air is 0.876.

Often convert dose in air to dose to medium: $\frac{D_{med}}{D_{air}} = \frac{(\mu_{en}/\rho)_{med}}{(\mu_{en}/\rho)_{air}} \cdot A $ where $A$ is the transmission factor equal to the ratio of the fluence at the measurement point $\Psi_{med}/\Psi_{air}$

$D_{med} = X \cdot \frac{\bar{W_{air}}}{e} \cdot  \frac{(\mu_{en}/\rho)_{med}}{(\mu_{en}/\rho)_{air}} \cdot A = f_{med} X A$

Charged particle equilibrium: CPE exists for volume v if each charged particle of given type/energy leaving v is replaced by an identical particle of same energy entering v. Difficult to measure dose without CPE. Fails around 3 MeV and above (range of secondary particles increases with radiation energy).
Conditions

1. Atomic composition of medium is homogeneous
2. Density of medium is homogeneous
3. There exists a uniform field of indirectly ionizing radiation (the rays are only negligibly attenuated by passage through the medium)
4. No inhomogeneous E/B fields are present

Transient CPE: when absorbed dose is proportional to (and greater than ) K_c.
Dose is less than collision kerma in buildup region (before d_max), then exceeds K_c shortly after, continues proportionally in equilibrium region. Lack of true CPE (D = K_c)because of attenuation: $D_{TCPE} = K_c e^{\mu' \bar{x}} \approx K_e (1+\mu' \bar{x})$ where $\bar{x}$ is mean distance the secondary charged particles carry their kinetic energy and $\mu'$ is the common slope of the D, K, K_c at depth.

Bragg-Gray cavity theory:

Relates the radiation dose in a cavity to the dose that would exist in a surrounding medium in the absence of the cavity.

Conditions

1. Dimensions of cavity should be small enough compared with the range of electrons that its presence does not perturb the charge particle field.
   - equivalent scattering properties of media
   - valid for primary charged particle beam or when charged particles are generated indirectly (photons)
2. The absorbed dose in the cavity is assumed to be deposited by crossing the cavity.

$D_m = D_g \cdot (\frac{S}{\rho})^m_g = \frac{Q}{m_g} \cdot \frac{W_{air}}{e} \cdot(\frac{S}{\rho})^m_g$, where the dose in medium $D_m$ equals the dose in the cavity (gas) $D_g$ times the ratio of the mass-electronic stopping powers of $m$ and $g$.
Stopping power is the energy lost by electrons per unit length in a material.

In practice the medium used is the wall of the ion chamber (e.g., graphite - conductive and tissue equivalent)

Spencer-Attix "restricted mass stopping power" uses a lower cutoff energy (usu. 10-20 keV for ion chambers), for electrons that do not enter the cavity.

Burlin cavity theory - adjustments to Spencer-Attix theory to allow for small and large cavities.
$D_g / D_w = d \cdot (\frac{S}{\rho})^m_g + (1-d) (\frac{\mu_{en}}{\rho})_w^g$ where $d$ is ratio of fluence of electrons generated in wall to that generated in the gas.

Dose equivalent: includes potential for biological damage, $H = D \cdot Q$

Radiation type	Quality factor
photons, electrons	1
protons	2
alphas	20
thermal neutrons	5
fast neutrons, heavier particles	20

Quality factor corresponds to linear energy transfer (LET) - energy transferred to medium per unit distance traveled (keV/μm).

Spatial distribution/transmission of radiation (photons, protons and electrons)

Attenuation of photons

Attenuation is the removal of photons from a beam (decrease in intensity) as they pass through matter. Caused by absorption and scattering of the primary photons, through the interactions described above.

Linear attenuation coefficient (μ): The fraction of photons removed per unit thickness of material. Value depends on the energy of the photons and the characteristic of the material.
$n = \mu \, N \, \Delta x$
where $N$ is the number of incident photons, and $n$ is the number of photons removed from the beam after traveling distance $\Delta x$
$dN/N = \mu \, dx$ → $ N = N_0 e^{-\mu x}$ where $N_0$ is the original number of photons, and $N$ is the number of transmitted photons.
The linear attenuation coefficient is the sum of the contributions from each of the interactions above (Rayleigh, photoelectric, Compton and pair production).
$\mu$ typically decreases with increasing energy (except at absorption edges). Increasing density increases $\mu$ (e.g. water has higher value than ice).

Mass attenuation coefficient (μ/ρ): linear attenuation coefficient decoupled from the density (normalized by density). Correspondingly, thickness $x$ becomes mass thickness (mass per unit area, e.g. g/cm²).

Half-Value Layer (HVL): thickness of a material required to reduce intensity by one half (attenuate half of the initial photons). Depends on energy, and is thus a measure of the beam quality (energies in the beam). Measured for narrow beams, so as to exclude scattered photons.
Tenth-value layer (TVL) is the corresponding value to reduce intensity to 1/10 of the original value (typically used in shielding applications).
For $n$ half values layers, the reduction in intensity can be calculated as $(1/2)^n$, assuming a narrow mono-energetic beam. E.g., 5 HVLs corresponds to 97% attenuation.
$HVL = \ln(2)/\mu$

Effective energy: characterization of a polyenergetic beam by the energy of the mono-energetic beam that would have same penetration.
Most x-ray beams are polyenergetic, so the HVL is used to characterize the beam quality (penetration or effective energy). Often measured as millimeter aluminum (mmAl). E.g. 50 keV ~ 6.97 mm Al, 100 keV ~ 15.06 mm Al.

Mean free path: averaged distance traveled before interaction
$MFP = 1/\mu = 1/(ln(2)/HVL) = 1.44 HVL$

Beam Hardening: Increase in average energy of a polyenergetic beam as the lower energy photons are preferentially attenuated. Overall the spectrum shifts to higher energy.
Homogeneity coefficient is the ratio of first HVL to second HVL, typically 0.5-0.7 for diagnostic x-rays.

Broad-beam buildup factor: Correction that accounts for the effects of scatter around the beam and to detector. B = quantity from scattered and secondary radiation divided by quantity from primary radiation. Can apply to quantities such as number of particles, dose, energy fluence. B for narrow beam or no attenuator is 1. B for broad beam in attenuator is greater than one.
Attenuation correction: $I_L/I_o = B\,e^{-\mu L}$. $B$ generally increases with depth, $L$, and attenuation coefficient, $\mu$.
Even at $L_o$ (surface) $B_0 > 1$ because of backscatter.

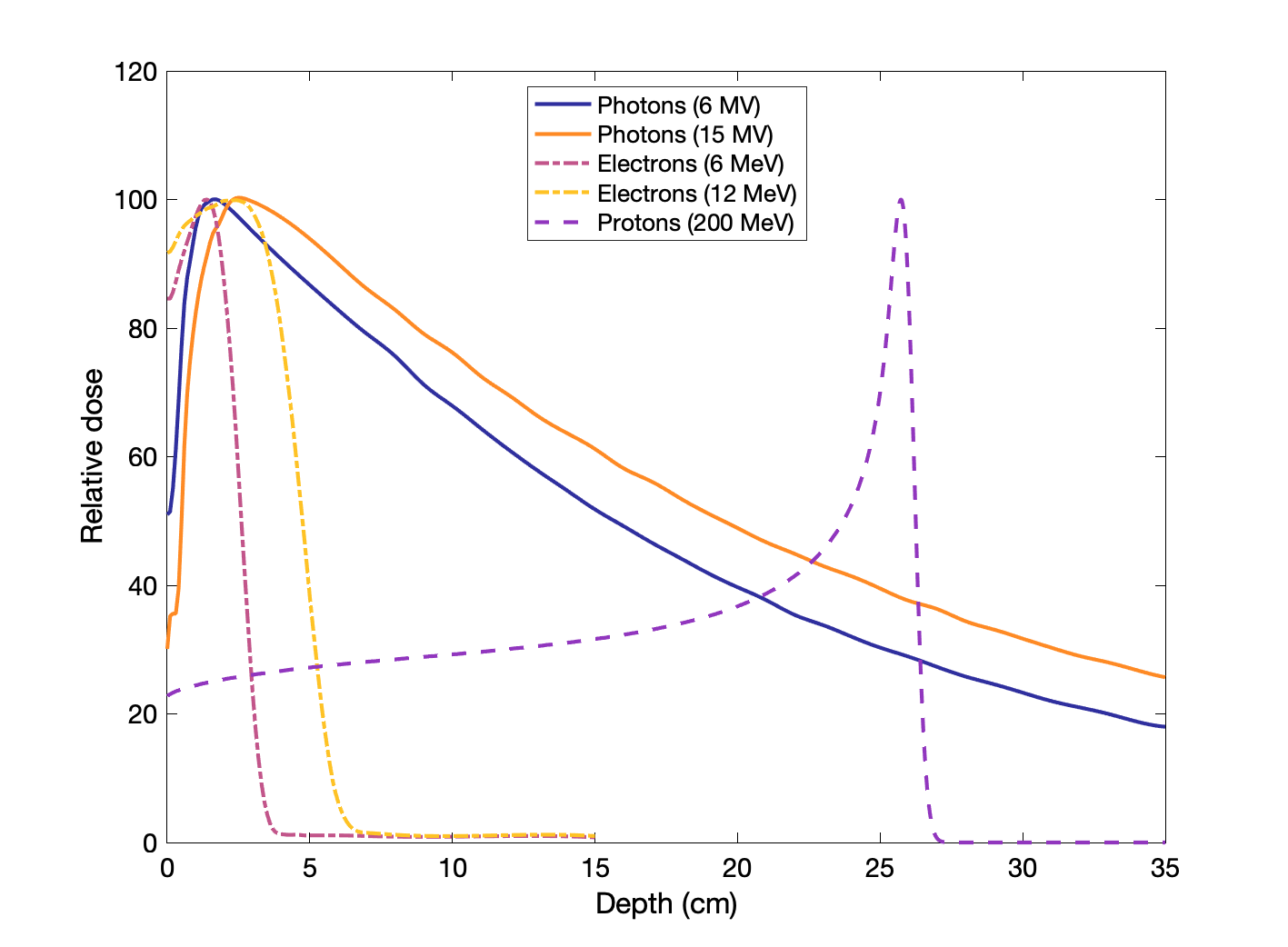
Percent dose depth curves for photons, electrons, and protons

Charge, mass, and energy affect how particles deposit dose with depth, as illustrated below:

Important dependencies

Compton scattering ∝ electron density = N_A Z / A
Higher energy → more forward scattering, more energy to electron

Photoelectric effect ∝ Z³/E³

Pair production ∝ Z ln(E)

Too many neutrons: n → p + β− + ν (beta-minus decay)
Too many protons: p → n + β+ + ν (positron emission) or p+e− → n + ν (electron capture)

Activity = λN = ln(2)/T_1/2 N

Cumulative activity = initial activity * mean time

Saturation activity = Σ⋅Φ = cross section * flux density (area * number per unit area per unit time)

Specific activity = activity / mass = λN/m

Bremsstrahlung energy efficiency ∝ ZE 
Rate of energy loss from bremsstrahlung is ∝ E_e and ∝ Z²/m²

Photon attenuation follows exponential decay depending on linear attenuation (depends on photon energy and material) and distance traveled.