Therapeutic Medical Physics

Clinical linear accelerator principles, collimation and mechanical aspects

Kilovoltage units - imaging and superficial (5 mm) therapy, up to 300 kVp, SSD 15-20 cm.

Orthovoltage units - 150 - 500 kV, SSD ~ 50 cm, ~90% before 2 cm depth

Megavoltage units - >=1 MeV, can include Co-60 gamma teletherapy (γ rays of 1.17 and 1.33 MeV).
Co-60 mostly used for gamma knife, MRI/Co therapy, developing countries, TBI
Has large penumbra, shallow dose, low dose rate.

→ Linear accelerators (linacs) most common now.

X-ray tubes have limit of 2-3 MV before electrical breakdown in power circuits → need linear accelerator for higher energy photon (and electron) beams.

Power supply, modulator and pulse forming network, pulsed microwaves (3000 MHz) produced in magnetron or klystron (higher power, more resilient), injected into accelerator tube (using waveguide). With pulse network coordination, electrons ejected from electron gun into the accelerator. Pencil beam of electrons bend 270 (to prevent spreading) and to treatment nozzle. Nozzle includes primary collimator, flattening filter or scattering foil (electron beam treatments), ion chamber (calibrate doses), secondary movable collimators, multi-leaf collimators (MLC), applicator (electrons only).

Modulator
Pulse forming network. High voltage pulses to microwave generator.
Thyratron: high voltage switch
Controls both electron gun and magnetron/klystron, provides same frequency of microwaves.

Magnetron: RF generator
Central heated cathode, anode of solid copper, pulsed DC field between.
Coaxial field from permanent magnet.
Electrons spiral and generate microwaves (resonant)
Power: 4 MW for 4 MV beam.

Klystron: RF magnifier
Two cavities separate by drift tube
Low level microwaves input, electron bunches from cathode to amplify to high power microwaves.
Microwave amplified with power up to 24 MW
Higher energy linacs, need oil tank in insulation.

Electron gun
Produced electrons to enter waveguide at correct time and phase
Triode gun allows rapid switching of injector current.

Waveguide
Main accelerator structure, uses high power RF, made of copper (conductive, thermal exchange).
Waveguide width (cross section) is proportional to the wavelength of the microwaves, around 10 cm (resonant frequency of ~3 GHz)
Length determines highest photon energy
Cavities allow acceleration of about 1 MeV/cavity

Traveling waveguide
Long and thin, good clearance.
Position changes with time.

Standing waveguide
Shorter, bulkier.
Amplitude changes with time (forward and backward traveling)

Gantry head
Steer beam - 270 degree backward circle (using bending magnets) to redirect beam at 90 degree angle without spreading (smaller focal spot, 1-2 mm) and better energy selection.
produce x-rays - target (W, Au) + flattening filter of lead, copper, aluminum (remove forward peak)
produce electron beam - no target + scattering foil (on carousel with FF)
control beam output - Ion chamber below carousel and above jaws, automatic feedback (servo) on MU and symmetry
shape beam - Jaws, MLCs, blocks, wedges (see below)

to the top

Clinical kV and MV photon beam characteristics

Photon beams usually described by peak electron voltages (thus peak photon energy), kVp. Mean energy is usually about 1/3 kVp

Treatment beams consist of photons of a range of energy, and that distribution is often called the "quality" of the beam.

Quality can be described in terms of half value layer (HVL), or the thickness of a material to attenuate a beam to half its initial intensity. Material is usually copper or lead.

Because of beam hardening (lower energy photons preferentially attenuated), the first HVL is usually thinner than subsequent layers.

In MV range, quality is usual described by peak energy and not HVL (except in radiation protection calculations). Already been heavily filtered.

$HVL = ln(2) / \mu = 0.693 / \mu$
$TVL = ln(10) / \mu = 2.3 / \mu$

HVL is measured with narrow beam with large distance between absorber and detector to limit scatter effects.

Peak energy (MV) can be measured directly (scintillation spectrometry or by photoactivation of appropriate foils), or indirectly (compared percent depth dose distribution in water with published data)

Depth of maximum dose changes with beam energy:
(also decreases slightly for increasing field size)

Energy	D_max
⁶⁰Co	0.5 cm
4 MeV	1.0 cm
6 MeV	1.5 cm
10 MeV	2.5 cm
15 MeV	3.0 cm
25 MeV	4.0 cm

to the top

Dose functions: PDD, TAR, TPR, TMR, SMR

Absorbed dose varies with depth for photons and particles. The dose depends on beam energy, depth, field size, distance from source, and collimation.

Percentage depth dose (PDD): $\text{PDD}(d,r,SSD) = D_d / D_0 × 100%$
Reference depth $D_0$ is 0 for orthovoltage and below (<400 kVp). The peak dose is used for higher energy beams ($d_0 = d_m$).
Note: peak dose varies with field size, and is determined for a small (3 × 3 cm) field with little electron contamination.

PDD decreases with depth $d$
PDD increases with beam energy (beyond buildup region, since peak dose shifts deeper). Mostly determined by difference in attenuation.
Peak dose roughly corresponds to electron range in the material.
PDD increases with SSD (i.e., dose relative to peak increases, while total dose decreases) because of inverse square law
PDD increases with field size $r$, less so for high energy beams with less side scatter. Typically tabulated for various square field sizes.

Source to surface distance (SSD).
Source to axis distance(SAD) is source to isocenter (axis of rotation) distance.
Geometric field size is determined at a specific SSD.

Equivalent square: equivalent square size for a given rectangular field with sides of length $a$ and $b$, based on having the same ratio of area to perimeter: $\text{A}/\text{P} = \frac{a\,\times\,b}{2(a\,+\,b)}$
Square side $c$ for an a × b rectangle: $c = 4 \cdot A/P = \frac{2\,a\,\times\,b}{(a\,+\,b)}$
Circular radius: $r = 4/\sqrt{\pi} \cdot A/P$ and $s = r \times \sqrt{\pi}$
These formulas are approximate!

Mayneord F factor: Accounts for changes in PDD with SSD (does not include scatter effects)
$F = \left(\frac{f_2+d_m}{f_1+d_m}\right)^2\left(\frac{f_1+d}{f_2+d}\right)^2$ where $f_1$ and $f_2$ are the two different SSDs and $d_m$ is depth of max dose.

Tissue-air-ratio (TAR): Ratio of dose in phantom at a given point to the dose in free space at that point: $\text{TAR}(d,r_d) = D_d / D_{fs}$
Accounts for attenuation and scattering (distance independent, inverse square factor cancels out).
Depends on field side $r_d$ at depth $d$.
No SSD dependence (useful for rotational delivery with varying contour).
Can only be measured for low energy (e.g. Co-60) beams.

Backscatter factor (BSF): TAR at maximum dose depth. Increases with field size. Peaks for beams with HVL(Cu) of ~0.7 mm and about 1 for > 8 MV beams.

$PDD = TAR \cdot 1/BSF \cdot \left(\frac{f+d_m}{f+d}\right)^2 \cdot 100$

Scatter-air-ratio (SAR): Ratio of scattered dose in phantom to dose in free space at same point. I.e., difference between dose at point minus 0 sized field dose at point.

$\text{SAR}(d,r_d) = TAR(r,d_r) - TAR(d,0)$

Collimator scatter factor (S_c): "In air output ratio", output in air relative to a reference field size, e.g., 10 × 10 cm.
Measured with ion chamber with buildup cap at SAD. Field size should exceed cap by 1 cm.

Phantom scatter factor (S_p): Scatter from phantom relative to reference field size. $S_p(r) = BSF(r) / BSF(r_0)$ where $r$ is size of field and $r_0$ is size of reference field.
Indirectly measure by dividing total scatter factor by collimator scatter factor.

Tissue phantom and tissue maximum ratios (TPR / TMR): Ratio of dose rate at a given depth to dose rate at a reference depth, for the same source to point distance (i.e., phantom shifts, point remain in place). TPR uses any reference depth, TMR uses the depth of maximum dose for reference. Max dose depth depends on field size and SSD (electron contamination).
Can be used for higher energy beams (unlike TAR).

Maximum dose depth ($d_m$) decreases with field size and increases with SSD (more electron contamination near surface for larger fields and closer sources). Set based on small field and large SSD.

$\text{TMR}(d,r_d) = (\frac{P(d,r,f)}{100}) (\frac{f+d}{f+d_{m0}})^2 (\frac{S_p(r_{m0})}{S_p(r_d)})$

TMR/TPR (isocentric): detector position relative to source is fixed. Depends on depth and field size at depth
PDD (fixed): surface position relative to source is fixed. Depends on depth, field size at surface, and SSD.

To calculate dose:

Equivalent square (EQS) table (at surface if fixed ssd or calc point if iso)
TMR table (isocentric) for given energy and depth
PDD table (fixed SSD) for given energy and depth
Scatter factors Sc and Sp or St and Sc for field sizes (EQS)
Info about calibration conditions

to the top

Monitor Unit Calculations

Typically use either SAD or SSD techniques

Isocentric

$MU = \frac{D}{ D_{cal} \cdot S_c(r_c) \cdot S_p(r_d) \cdot TPR(d,r_d) \cdot WF(d,r_d,x) \cdot TF \cdot OAR(d,x) \cdot (SCD/SPD)^2 }$

Non-isocentric

$MU = \frac{D}{ D_{cal} \cdot S_c(r_c) \cdot S_p(r) \cdot PPD(d,r,f)/100 \cdot WF(d,r_d,x) \cdot TF \cdot OAR(d,x) \cdot (SCD/f+d_0)^2 }$

where:

$D$ = dose, $D_{cal}$ = calibration dose per MU at $d_{ref}$ under reference conditions

$S_c(r_c)$ = collimator scatter factor for collimator field size $r_c$

$S_p(r)$ and $S_p(r_d)$ = phantom scatter factor for field size of $r$ at surface or $r_d$ at depth $d$

$WF(d,r_d,x)$ = wedge factor at depth $d$ for field size $r_d$ and off-axis distance $x$

$TF$ = tray factor (tray for holding blocks, independent of field size and depth)

$OAR(d,x)$ = Off-axis ratio at depth $d$ and off-axis distance $x$

$SCD$ = source to calibration point distance (at which $D_{cal}$ is defined)

$SPD$ = source to point of interest (at which $D$ is delivered) - inverse square correction

$d_0$ = reference depth ($TPR$,$PDD_N$) or max dose depth ($TMR$, $PDD$)

St: measure in phantom with given field size relative to reference size
Sc: measure in miniphantom with given field size relative to reference size
TPR: measure in phantom at depth d relative to dref (isocentric, constant SAD)
PDD: measure at depth d relative to dmax, same SSD or SAD
INV: inv square to d vs at dmax
TAR: measure dose in phantom vs dose in air (isocentric)
OAR: measure x distance from axis for all else same

to the top

Principles of radiation treatment planning

See above for basic MU calculations.

Isodose distributions - lines that pass through same dose, usually shown as relative to a reference point.

Similar penumbra for beams from 1 MV to 10 MV. Flatness changes slightly with depth (flattening filter hardens central beam). Typically have 3% flatness in at least 80% of field.

Flattening filter free (FFF) beams used for small fields (radiosurgery) and in some IMRT cases. Higher fluence rate → shorter treatment times, less scatter, fewer neutrons.

Wedge filters: physical or virtually created collimating jaws to tilt the isodose curves toward the thin edge. Degree of tilt depends on wedge angle. Thinner side has deeper doses. Essentially a method of intensity modulation; can be used to reduce hot spots and improved uniformity of combined fields.
Lead or steel placed above second jaws. Typically 60 degrees. Can combine wedge with open field to get other angles. Wedge isodose angle defined as isodose tilt relative ot the central axis at a specific depth.
Wedge factor (WF): ratio of doses with and without filter at a given depth on central axis.

Field configurations

Optimize dose to tumor vs normal tissues by using correct size, number of fields, ideal beam directions, adjusting beam weights, appropriate energies, useful beam modifiers (wedges, compensators).

Parallel opposed: same axis from different directions. Simple, reproducible, uniform dose to tumor, unlikely to miss. Lower energies lead to higher peripheral doses. Not much peripheral sparing.

Multiple fields: 4 fields, opposing and perpendicular; 4 fields, oblique; three fields, e.g., anterior and two posterior obliques;

Choice of fields depend on tumor location, nearby critical organs, setup accuracy.

Rotation therapy best for small, deep seated, centrally located tumors.

Wedges useful to reduce peripheral hot spots, especially for shallow targets irradiated from one side only.

Tumor dose specifications

Volumes typically defined: GTV, CTV, ITV, PTV, original developed by ICRU

Gross tumor volume (GTV): Bulk of the tumor, easily defined by imaging, along with involved lymph nodes and possibly metastatic regions. Post-operatively, typically the outline of the resected region.

Clinical target volume (CTV): Includes GTV and other tissue presumed to have tumor cells (true extent beyond what can be seen in imaging, "subclinical").

Internal target volume (ITV): Margin added to account for internal movements or variations of the target relative to the reference system.

Planning target volume (PTV): Includes CTV+ITV plus a margin of error for setup uncertainties.

Organ at Risk (OAR): Nearby organs that need protection from excessive dose. Are also contoured and avoided as much as possible without compromising tumor coverage. May also need a planning margin.

Treated volume: Often slightly larger than PTV, to ensure minimum isodose coverage

Irradiated volume: Volume receiving at least 50% of target dose. Larger than treated volume.

Maximum target dose: Highest dose covering at least 2 cm².

Target dose typically specified at a reference point: clinically relevant, representative, easy to define unambiguously, can be accurately calculated, not near a steep dose gradient. Usually try to place long a central axis or center of rotation.

Irradiation technique includes

radiation quality (beam energy)
SSD or SAD
field sizes
beam-modification devices (wedges and shielding blocks, etc.)
beam positioning and weighting
correction for tissue heterogeneities
dose fractionation
patient positioning

Radiographic simulator may be used for simple cases and emergency treatments. Simulators replicate the geometry of the treatment machine, but use imaging x-rays.

More commonly today, contours for the treatment volumes and critical organs are typically generated on CT simulator and/or MRI images.
The CT simulator has lasers and bed motions that can be replicated during treatment.
The 3D CT images are converted into digitally reconstructed radiographs (DRRs) using virtual source and virtual film that can be compared to radiographs taken during treatment setup.

Setup is done with the help of port films (images take using the treatment machine, usually low quality because of high photon energy), orthogonal x-rays next to the machine, or cone-beam CT (CBCT).

Electronic portal imaging devices (EPIDs) commonly used, typically made of flat panel arrays of solid state detectors: scintillator, light collected by photodiodes, on amorphous silicon panel (radiation hard).

CBCT are typically mounted on gantry (kV x-ray source) and use a flat panel detector.

Surface irregularities (now typically handled with commercial computer dosimetry):
For PPD, adjust based on inverse square distance: $P' = P \cdot \left(\frac{SSD + d_m}{SSD + d_m + h}\right)^2$ to add/subtract $h$ to true SSD.
For TAR(d,r_d)/TMR(d,r_d), adjust parameter $d$ → $d+h$ where $h$ is difference of new surface from reference surface. Also need to adjust $r_d$ to $r_{d+h}$

Compensators can be used to smooth out irregularities. Size of compensator needs to be adjusted based on placement within beam (to account for divergence)

Inhomogeneities: changes in absorption (affects area beyond), scatter (affects area near), and secondary electron fluence (affects area within and near).
In MV range, attenuation is based on electron density → use effective depth
Lose electronic equilibrium near low density regions
Ortho and energies below have higher doses within and near bone (photoelectric effect).

Convert $d$ to water equivalent depth: e.g., $d_{total} = d_1 \cdot \rho_1 + d_2 \cdot \rho_2$
Then can use in PDD and TMR calculations.
Isodose shifts towards skin for bone and away for air. Roughly ±0.5× the thickness of inhomogeneity.

Within inhomogeneity: ratio of f-factors, i.e., $\left(\frac{\mu_{en}}{\rho}\right)^{tissue1}_{tissue2}$ (energy dependent!)
Orthovoltage: increased dose within bone, lower after
Co-60: lower dose in bone and after

Dose to soft tissues in bone: enhanced by ratio $\gamma = D_{STinB} / D_{ST} = \left(\frac{\mu_{en}}{\rho}\right)^B_{ST}\cdot\left(\frac{S}{\rho}\right)^{ST}_B$
Stopping power is greater for soft tissue than bone at all energies (more electrons / mass)
Mass absorption is greater for bone at low (photoelectric) and high (pair production) energies.

Bone in ST: enhance dose for a few mm before interface (backscatter electrons), roughly indep of MV energy. After bone, at lower MV, dose lower than without bone, but then gets higher. At higher MV, dose higher than without bone (pair production).

Air cavity: underdose around cavity. ≤10% at Co-60 energies. Larger effects for higher energies and small fields. ?????

Field shaping, field separating

Shielding blocks can be used to conform field to target, typically made of lead. Transmission of 5% is acceptable: $1/2^n = 0.05$ where $n$ is number of HVLs needed → $n = log(20)/log(2) = 4.32$. About 5 cm needed for Co-60, 6.5 cm for 6 MV, and 7 cm for 10 MV beam.
Typically placed on tray above patient. Tapered for divergence.
Cerrobend used for custom blocks (bismuth, lead, tin, cadmium with high density, low melting point). Needs to be 1.21× as thick as lead.

Multi-leaf collimators (MLC): More modern method of beam shaping. Many (60-80) ~ 1cm tungsten alloy leaves can be moved in and out to generate desired beam shape(s). Edges usually rounded to account for divergence. Can create slightly jagged field (makes matching multiple fields difficult).
Especially useful for intensity modulated radiation therapy (IMRT) since they can be dynamically controlled.

Electron contamination can result in increased surface dose. Produced in collimators, filters, wedges, tray. Need small dosimeter in build up region sharp gradient) - typically parallel plate ion chamber (design dependent response). Can also use TLDs.

Skin dose
Placing scatterers (e.g., shadow tray) further from patient reduces skin dose (divergence, scatter, attenuation).
Skin dose depends on field size: Larger field, higher percent surface dose (electron contamination)
If skin dose is needed a bolus material can be used to build up the dose to that is peaks at the skin.
Absorbers with Z ~ 50 (tin) can reduce extra skin dose from lucite trays.
Skin dose increases with angle of incidence - electron range surface: ellipsoid around photon beam. At oblique angles the oval enters skin. Also, maximum dose occurs are shallower regions.

Adjacent fields

Care must be take in junction region of two fields to avoid hot and cold spots. Also should aim to not overlap field in region of tumor or critical structure

Avoid overlap from geometric divergence if possible: angle beams away, slightly separate fields on skin surface, split beam with collimator/block, penumbra generators.

For parallel but divergent beams joining at depth $d$: Separation given by $S = \frac{1}{2} \cdot L_1 \cdot\frac{d}{SSD_1} + \frac{1}{2} \cdot L_2 \cdot \frac{d}{SSD_2}$ where $L$s are the field length at the surface and $SSD$s are the source to surface distances.

Can angle beams or rotate collimator to match divergent edge to edge of the other field. Can also rotate couch as necessary.

Field lines should be drawn for each treatment based on first field - some small daily variation is good and sometimes used deliberately to smear junction.

Dose modeling

TERMA â¨‚ dose deposition kernel = Absorbed dose
TERMA is energy removed from primary beam per unit mass - need beam fluence
Kernel must be calculated, based on energy.
Kernel hardening, tilting, density scaling.

Collapsed cone convolution: improve computation speed. MN³ where M is number of directions (cone).
Discretize directions into M cones, no 1/r² dependence.

AAA—Analytical Anisotropic Algorithm (varian)

Dose volume histograms (DVH): % of volume receiving dose D.

D95: dose received by 95% of volume
V20: volume receiving at least 20 Gy

QUANTEC = Quantitative Analysis of Normal Tissue Effects in the Clinic
Determine normal tissue dose limits.
Give limits on Dmax or mean dose for rates of various endpoints

to the top

Clinical megavoltage electron beam characteristics

Typically use electrons in 6 to 20 MeV range, from same linacs as photons (but almost monoenergetic). Electrons are used for superficial (< 5 cm deep) tumors, often for face, head and neck, breast boost, and nodal boost.
Because electron dose falls off abruptly stop at a given depth depending on energy, the choice of initial energy is very important.

Energy loss of electrons is mostly ionization/excitation in low Z and bremsstrahlung in high Z.

Mass stopping power is higher in lower Z materials (more electrons / gram) and electrons not as tightly bound.

At ≥1 MeV rate of energy loss is ~2 MeV/cm in water. Range in water is typically used to characterize the initial electron beam energy.

Rate of energy loss from bremss is $\propto E_e$ and $\propto Z^2$

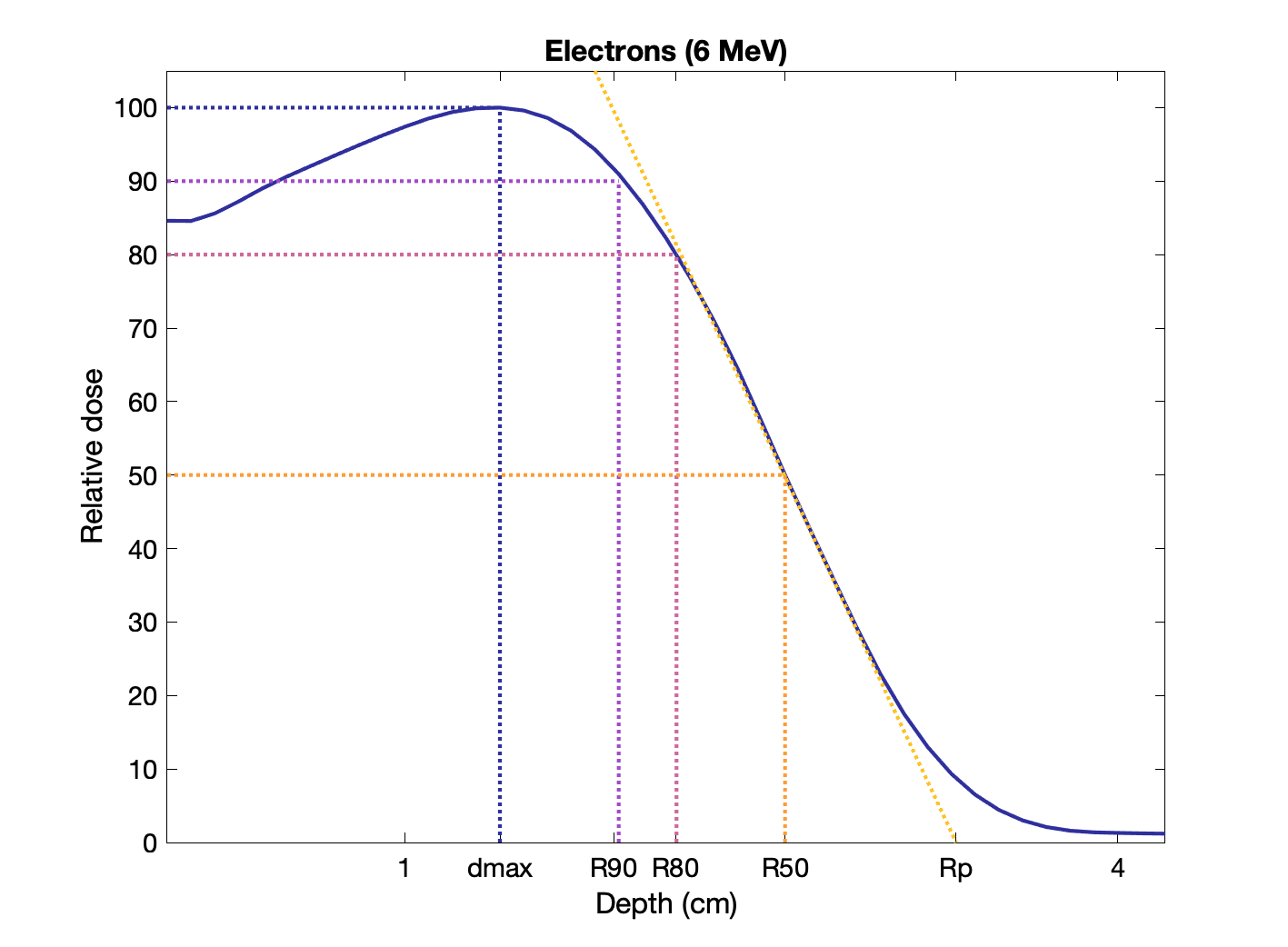
Percent depth dose of electrons (6 MeV) with various ranges indicated:

Rules of thumb for electron ranges in water (E in MeV):
R90 ≅ E / 3.2 cm
R80 ≅ E / 2.8 cm
R50 ≅ E / 2.33 cm
Rp ≅ E / 2 cm

More energy is lost per gm per area in gas than in denser medium - polarization/screening effect.

Spread of beam (scattering) can be characterized by Gaussian distribution. Scattering power $\propto Z^2$ and $\propto 1/E^2_e$
Thin, high-Z scattering foils are used in linacs to spread the beam.

Most probable energy: defined at water phantom surface, given by $(E_p)_0 = C_1 + C_2 R_p + C_3 R_p^2$, where $R_p$ is the practical range in cm, the range where the dose falloff is extrapolated linearly to level of background dose. $C_1$ = 0.22 MeV, $C_2$ = 1.98 MeV/cm, $C_3$ = 0.0025 MeV/cm² for water. $R_p(cm) \approx E(MeV)/2 \text{ cm}$ in water and $\approx E(MeV)/2 \text{ mm}$ in lead.

Measurements are made with ion chambers, diodes or film to create a depth ionization curve which is then converted to depth dose.

Mean Energy: $\bar{E_0} = C_4 \cdot R_{50}$, where $R_{50}$ is the depth where the dose is 50% of maximum. $C_4$ = 2.33 MeV/cm or 2.4 MeV/cm.
Beam quality is specific by $R_{50}$.
$I_{50}$: point where intensity drops to 50% of $I_{max}$

Energy at Depth: Most probably energy and ~ mean energy decrease with depth
$(E_p)_z = (E_p)_0(1-\frac{z}{R_p})$ and $\bar{E_z} = \bar{E_0} (1-\frac{z}{R_p})$

Reference depth: $R_{ref} = 0.6 R_{50} - 0.1 cm$.
Depth at which measurements are made.

Output: absorbed dose per monitor unit (MU) at $d_{max}$ in a phantom.

Typically use same standards as photons: SSD = 100 cm, field size = 10 × 10-cm.
Calibrate to have 1 cGy / MU with these settings.

Increase SSD: output factor increases, slight change in PDD, significant increase in penumbra (depends on energy)

Ionization depth curve can be converted to a dose curve by correcting for difference in restricted mass stopping power of water vs air $(L/\rho)^{w}_{air}$, and the effect of the ion chamber.

Silicon diodes: are small and sensitive, but have temperature and directional dependence. Okay for relative dosimetry only (e.g., PDD) and silicon has similar mass stopping power, so don't need correction.

Film: can collect full isodose curves, with optical density proportional to dose. Okay for relative dosimetry only. Should have linear response in dose range used, and be processed carefully.

Conversion from other types of phantoms to water:

$D_w(d_w) = D_{med}(d_{med})(S/\rho)^w_{med} \Phi^w_{med}$ (assumes identical energy spectra, which typically isn't true)
Can use water-equivalent depths: $d_w = d_{med} \times \rho_{eff} = d_{med} \times R^w_{50} / R^{med}_{50}$

Characteristics of electron beams

Each machine will behave slightly differently, even for same nominal energy, so device specific calibrations are necessary.

Electrons need applicators or cone place closed to surface to block extraneous radiation.

Uniform dose region followed by rapid falloff. Gradient increases with increasing energy (less steep) and beam goes deeper. Beyond the electron range (2 MeV/cm loss), remaining dose is from photon contamination (bremsstrahlung in collimators and tissues, usually 1-5%). More photons for higher energies.

Depth in cm of 80% to 90% isodose corresponds to 1/3 to 1/4 of electron energy in MeV. (20 MeV → 5 to 6.7 cm useful depth)

Therapeutic range: 90% depth dose, ~ $(E_p)_0/3.2 \text{cm}$
80% depth dose ~ $(E_p)_0/2.8 \text{cm}$
$D_{max}$ does not vary linearly with energy.

Increasing energy → increasing surface dose (opposite of photon beams).

Uniformity and flatness (ratio of area where dose exceeds 90% of central value, ICRU) are described in a particular plane, typically at half the therapeutic range or 95% isodose.
Often use two foils (lead) to spread beam and then flatten.

Dose increases with field size (scatter). Small fields lead to a shift/tilt in PDD toward surface.
For lateral scatter equilibrium (LSE), need field size at least $R_{eq} \approx \sqrt{E_{p,0}}$

Field equivalence determined based on PDD shape (not output factor). High energy and broad fields generally have field equivalence.
Diameter equivalence for $a \times a$ field: $D_{eq} = 1.12 a$

Square root method: Depth dose for rectangular fields: $D^{x,y} = \sqrt{D^{y,y} \cdot D^{x,x}}$

Electrons diverge from a virtual (apparent) source, determined from the scatter foils and based on backprojections. Can use as virtual SSD for large fields only.
Effective SSD: effective source position to phantom position (e.g, isocenter). Depends on energy and field size but not on measurement depth.

Treatment planning considerations for electrons

Now typically done with computers, but may need manual double checking

Choose energy to cover target and avoid critical organs (e.g., set the chest wall-lung interface to 80% isodose in breast irradiations)

Field size should cover PTV, accounting for tapering of ≥80% isodose curves at higher energies (i.e., may need larger surface field).

Curved surface and air gaps between applicator and skin is a problem. Inverse square effect plus side scatter effects.
Beam obliquity tilts dose to suface and decreases depth of penetration (PDD tilts towards surface). Pencil beams "droplets" overlapping more. But skin dose may decrease?
For extra gap of g, $D(f+g,d) = D_0(f,d)\cdot \left(\frac{f+d}{f+d+g}\right)^2 \times OF(\theta,d)$ where $OF$ is the obliquity factor for beam angle of $\theta$. $OF$s are tabulated for various energies and angles.
Can get hot spots in areas on air gap side surface gradient. That is, electrons are scattered outward by steep projections and inward by steep depressions. Bolus (with tapered edges) can be used to smooth out a gradient.

Inhomogeneities will alter dose distribution. Difficult to characterize small regions, slabs can be corrected with coefficient of equivalent thickness, using electron density relative to water. Can also correct to effective SSD.

$d_{eff} = d - z(1-\rho_{m}/\rho_{water})$ for material of thickness z.

Small, higher scattering material will reduce dose directly behind it, but increase dose beyond to the sides of it.

Bolus and absorbers

Flatten irregular surface, reduced electron penetration, increase surface dose. Should be tissue equivalent (stopping and scattering).

Slabs, plates (PMMA), milled waxes, polystyrene sheets are all possible absorbers.

Adjacent fields

Need to be careful to avoid hot/cold spots at junction (same as for photons). Usually abut on the surface.

Electron + photon field: Hot spot on photon side, cold spot on electron side (out-scattering electrons).

Field shaping

Lead cutouts on skin or at end of cone. Less than 10 MeV, lead thickness < 5mm for < 5% transmission.
Measure transmission with parallel-plate ion chamber in polystyrene phantom.

Roughly, thickness of lead in mm should be E(MeV) / 2. Can add mm for safety. Cerrobend should be ~ 20% thicker.

Decrease in output factor to blocked beams. Effect is greater for higher energies. Affect PDD too.

Output factor: output variation with field size. Small factor for larger field sizes, but increases drastically for smaller fields (need to measure) - drops at sizes around 6×6 cm ≤ 10 MeV, around 10×10 cm for ≥ 12 MeV
For fields of size > $R_p$, size has little effect on depth dose (is at LSE).

Shielding material can also be place "internally" after the treated region (e.g., lip, eyelid, cheek).
Lead can cause electron backscatter. More backscatter for lower energies. Aluminum or wax between tissue and lead can reduce effect.

Electron Arc Therapy

Useful for curved surfaces (chest wall, limbs) - photons could go into lungs or long bones, abutting fields can have cold/hot spots.

Calibration: Integrate stationary beam profiles and/or measure directly.

Energy - more penetration than stationary
Field size - smaller (≤ 5 cm) for normal incidence, but lower dose rate and more x-ray contamination. Usually 4-8 cm at isocenter.
Isocenter - equidistant from surface as much as possible for all angles and greater than max electron range.
Shaping - Lead to sharped edges of arc field.

Total skin irradiation

Electrons of 2 - 9 MeV for superficial lesions over large areas (mycosis fungoides and other cutaneous lymphomas). Treats up to 1 cm in depth and spares bone marrow.

Translational - Patient on motor driven couch, moved as needed to cover body, anterior and posterior. Use 90Sr β or Van de Graff generator.

Large field - Scatter electrons through wide angles and use large distance to generate large field. Patient typically standing. Typically scattering through 4 m in air is sufficient to generate desired width of 1 m.

X-ray contamination can be limiting factor. Can angle the beam 10 to 15 degrees above/below horizon to limit (photons mostly directly along central axis).

Field arrangement: anterior, posterior, and four obliques.

Obliquity is a large factor and depth doses shift to surface. ~ 10% uniformity can be achieved with 6 fields.

Total body irradiation

Conditioning process for bone marrow transplantation (for leukemia, lymphoma, autoimmune diseases, aplastic anemia and mutiple myeloma)

Large field size, uses AP/PA, lateral, others

Patient stands or sits in immobilizers
Beam spoiler (1-2 cm acrylic) just in front is used to scatter beam (bring surface dose to 90% of prescribed)

AP/PA: lower energy, homogenous but less stable/comfortable, needs large room, need blocks for lungs, kidneys and brain.
Lateral: higher energy (15 MV), patient can lie or sit, smaller room, less homogenous, needs compensator for different thicknesses (on spoiler?).
Others: 4 sources, single source at short SSD, scanning source, scanning patient, source sweep, adjacent fields

Treatment planning algorithms

Originally based on ray line geometry of broad beams with empirical corrections for inhomogeneity.
Limited effectiveness on complex and small heterogeneities.

Pencil beam with multiple scattering - gaussian distribution based on Fermi-Eyges multiple scattering theory.

The pencil beam dose is given by $d_p(r,z) = d_p(0,z)e^{-r^2/\sigma_r^2(z)}$ where $d_p(0,z)$ is the axial dose, $r$ is the distance from the central axis, $z$ is depth, and $\sigma_r^2(z)$ is the mean square radial displacement of electrons as a result of multiple Coulomb scattering.

Dose from single pencil beam looks like a teardrop. Total dose is calculated from summing pencil beams. To integrate, need to use error function (erf).

$\sigma$ was predicted theoretically by Eyges using small-angle scattering of Fermi in a slab geometry (varying density).
Doesn't include large angles, assumes $\sigma$ increases with depth indefinitely.

CT numbers (by pixel) are used to correct for heterogeneity.

Clinical proton beam characteristics

Protons are heavy and charged - lose energy as they pass through matter and deposit most energy at end of path, the "Bragg Peak"

Stopping power is proportional to atomic number $Z$, square of particle charge $z$, and particle speed $\beta = v/c$
$dE/dx \propto Z\,z^2\,/\beta^2$
(more dose deposited when protons are slower, hence the peak at end of range)

Depth of dose depends on initial energy
$r_0$: Depth at which 50% of protons are stopped does not depend on energy spread (slope of curve does).
$r_0 \approx R_{80}$, depth of 80% of maximum dose (also independent of energy spread).
Width of Bragg peak depends on energy spread.

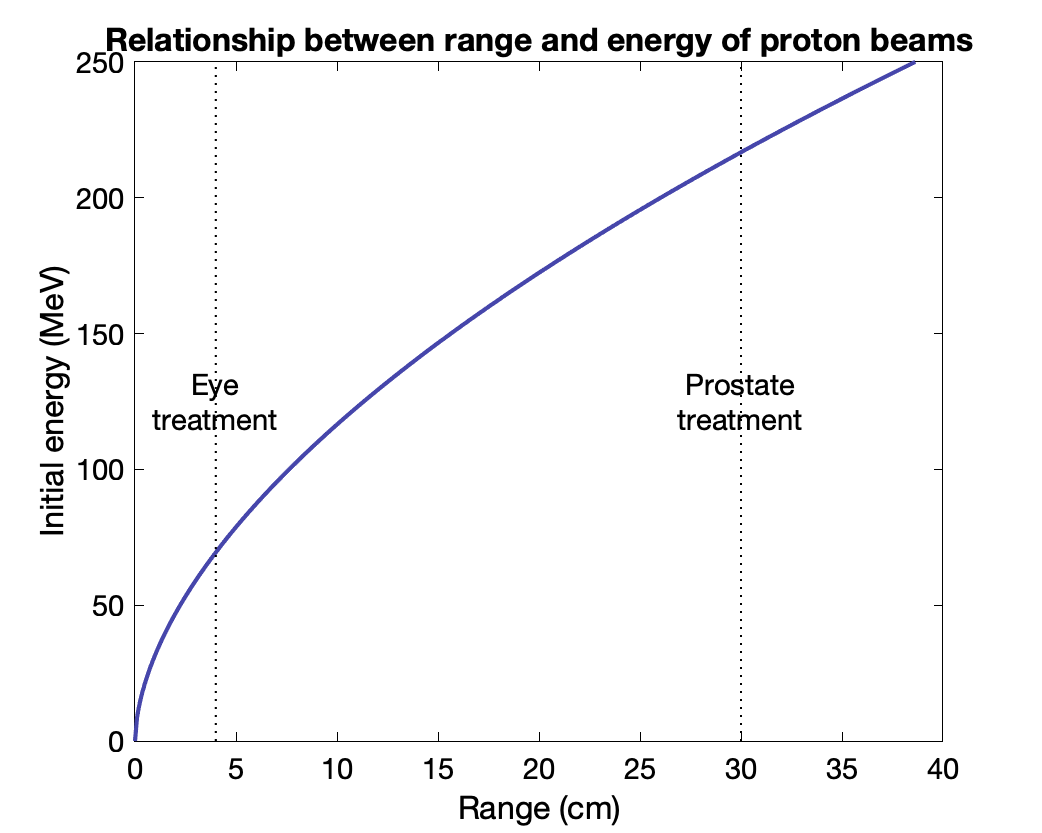
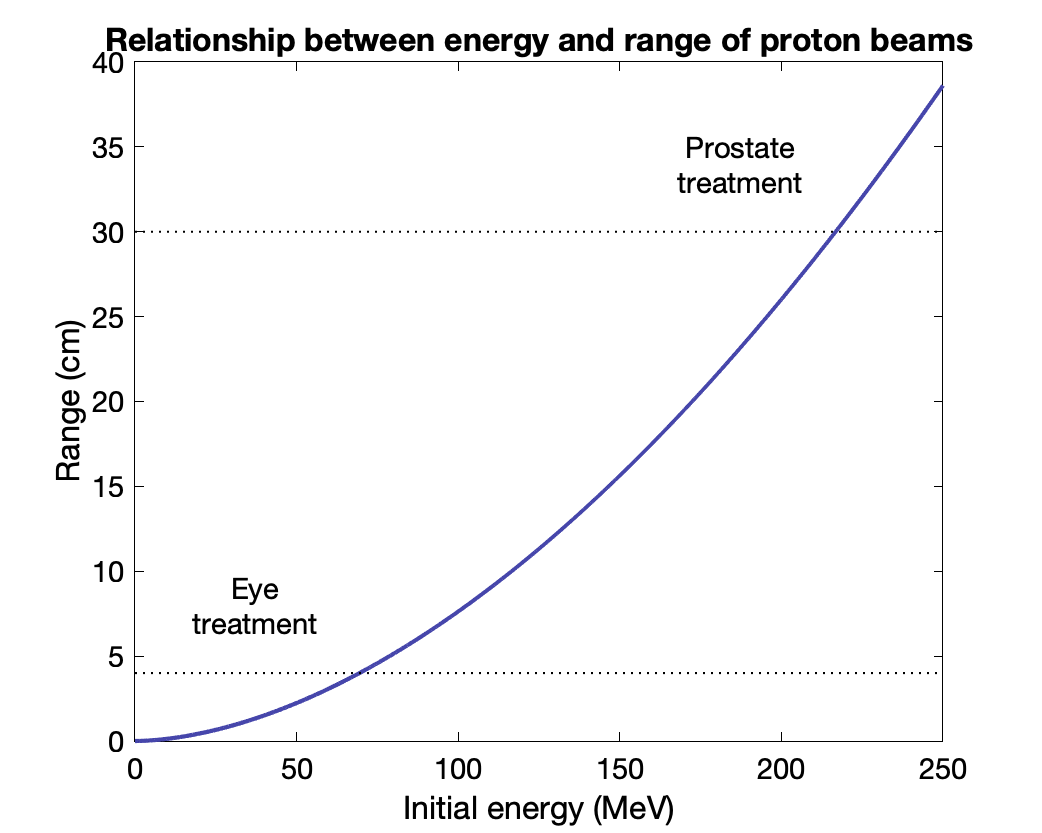
$T(R) = \frac{1}{a^{1/b}}R^{1/b}$ where $a$ = 0.0022 and $b$ = 1.77
Prostate at 30 cm → 216 MeV beam
Eye at 4 cm → 70 MeV beam

Spread out Bragg peak (SOBP using multiple energies) to cover target extent in depth.
Add multiple Bragg peaks with various weights to get homogenous dose in depth.
Multiple Coulomb scattering - beam spread with depth, larger penumbra.

Scattering
Modulator wheel + second scatterer to get homogenous spread of dose in depth, SOBP
Brass apertures cut out to define lateral beam dimensions (like a static MLC or block for photons)
Plastic compensator to change beam depth (not intensity!) in patient. Smeared slightly to cover tumor in spite of uncertainties, more distal dose.

Scanning
Deflection magnets to move beam to desired locations
Depth controlled by energy of beam, upstream to magnets
Dose at each point determined by intensity and/or time at each spot
Spot is Gaussian with size give by FWHM = 2.35 σ, with non-gaussian tails called "beam halo"
Beam can be continuous between spots, or turned off while moving to new spot.
Better at limiting entrance dose.
3-D painting of target possible. Intensity modulated proton therapy (IMPT) possible. Simultaneous integrated boost possible

Matching
Match beams at 50% isodose levels (lateral and distal)
With PBS, can feather each beam (rather than shifting) so overlap gives correct total dose.
Used for large tumors, CSI, head & neck, changing geometries (around critical organ, e.g., brain stem)
Can match to photon beams also.

Generated by cyclotron or synchrotron (linac needs too much power for heavier particles)
Cyclotron resonant frequency: $f = \dfrac{qB}{2\pi m}$
Isochronous: B with radius. B = 3, 6, 9 T
Synchro: decrease RF frequency over time

Heavier particles

Range of heavier ions relative to proton range: $R_{ion} = R_p \cdot M_{ion} / M_p \cdot z^2$
(continuous slowing down approximation, CSDA)

Comparison of clinical photon, electron and proton beams

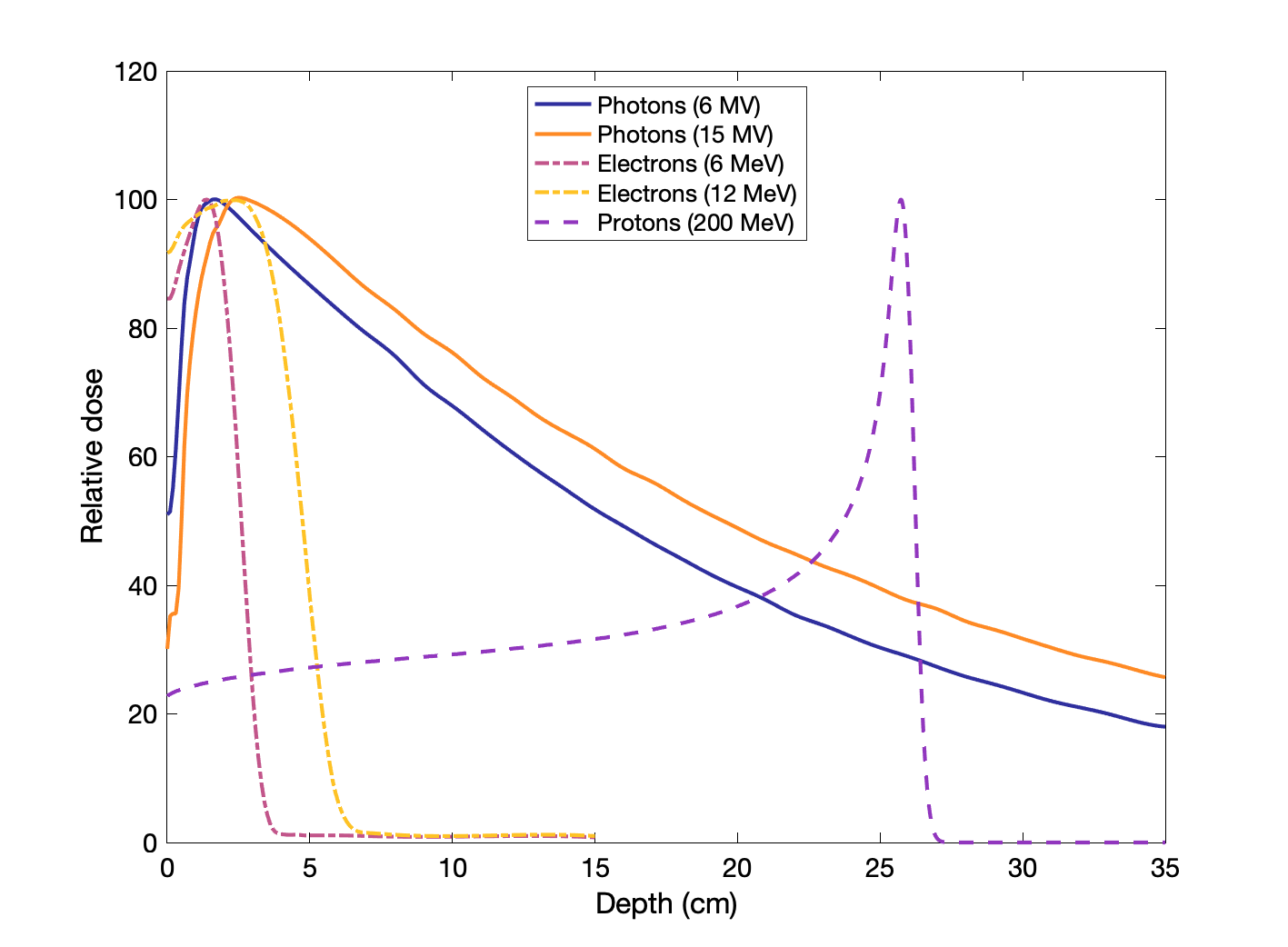
Percent dose depth curves for photons, electrons, and protons

Charge, mass, and energy affect how particles deposit dose with depth, as illustrated below:

Higher energy for charged particles means more depth.
Higher energy for photons means deeper location of max dose and lower entrance dose.
Higher mass for charged particles means sharper Bragg peak (electrons are very light, so it is not really a peak).
Neutron PDDs have similar shape to photons (both are neutral).

Lateral distribution

Protons tend to have sharper lateral profiles (smaller penumbra) than electrons or photons.

Brachytherapy

Brachytherapy uses sealed radioactive sources that deliver radiation within a short distance, including interstitial (implanted seeds), intracavitary, or surface applications. Can also be combined with external beam therapy.

Isotopes include ²²⁶Ra,²²²Rn, ¹³⁷Cs, ¹⁹²Ir, ¹⁹⁸Au, ¹²⁵I, ¹⁰³Pd.

Radionuclide	Half-life	Photon energy (MeV)	Half value layer (mm lead)	Exposure Rate Constant (R-cm²/mCi-h)
²²⁶Ra	1,600 y	0.047-2.45 (0.83 avg)	12.0	8.25
²²²Rn	3.82 d	0.047 – 2.45 (0.83 avg)	12.0	10.15
⁶⁰Co	5.26 y	1.17, 1.33	11.0	13.07
¹³⁷Cs	30.0 y	0.662	5.5	3.26
¹⁹²Ir	73.8 d	1.36 – 1.06 (0.38 avg)	2.5	4.69
¹⁹⁸Au	2.7 d	0.412	2.5	2.38
¹²⁵I	59.4 d	0.028 avg	0.025	1.46
¹⁰³Pd	17 d	0.021 avg	0.008	1.48

The usefulness and application for various isotopes depends on the particle types emitted, their energies, and the half-lives.
For instance ²²⁶Ra goes through multiple decays, releasing α, β and γ particles, but α and β particles are filtered out and only the photons are used.

Many sources are specified by

actual length in mm
active length in mm
activity/strength in mgRa or mCi
filtration (wall thickness/material) in mm Pt

Radiographs and autoradiographs (exposing film to the source) can be used to test distribution.

Exposure rate constant: relates activity (e.g. Ci or Bq) to exposure (R). Usually given as exposure rate in R/h at 1 cm from 1 mCi point source. Not always well defined.

ICRU "air kerma rate constant": $\Gamma_\delta = \frac{l^2}{A}\left(dk_{air}/dt\right)$, SI units: $m^2-J/kg = m^2-Gy/Bq/s$

Longer-lived isotopes are typically used for temporary implants and afterloaders

²²⁶Ra (with 0.5-mm Pt filter): $\Gamma_\delta$ = 8.25 R-cm²/h/mg
¹³⁷Cs: mono-energetic γ-emitter, similar uses to radium, roughly same penetrating power
¹⁹²Ir: Often used in afterloaders.
¹⁹⁸Au: Short half live, permanent interstitial implants possible (replaced ²²²Rn, which have residual betas and brems photons)
¹²⁵I: Permanent implants (replaced gold and radon). Longer half-life (more convenient). Various encapsulation methods, complicated dosimetry.
¹⁰³Pd: Newer, similar to ¹²⁵I but shorter half-life means faster dose delivery.

Source strength usually given in mCi. Exposure rate is proportional to activity × exposure rate constant.

Measure exposure rate at a known and sufficient distance to consider source as a point source (e.g. 1 meter). Minimize geometry dependence.

Convert to mgRa by dividing by exposure rate constant of radium filtered by 0.5 mm Pt: 8.25 R-cm² / mCi-h

Apparent activity: bare point source activity (exposure rate at 1 m / bare exposure rate constant at 1 m).

Air Kerma Strength: $S_k = \dot{K_l}\cdot l^2 = \dot{X}\cdot (\bar{W}/e) \cdot l^2$, where $\dot{K_l}$ is air kerma rate and $l$ is distance of calibration point.
Units: μGy-m²/h
(AAPM recommended quantity for specifying brachytherapy sources)

NIST calibrations using large spherical graphite cavity chambers. Compared to standard sources.
Well-type ion chambers for routine calibration (relative to exposure calibrated sources of same kind).

AAPM TG-43U1: (updated) protocol for brachytherapy dose calculations.

Exposure rate at a point near a brachy source is determined using the Sievert integral (inverse square w/linear geometry and filtration effects). Depends on source activity, exposure rate, constant (unfiltered), length, filtration, effective attenuation of filtration, distance from center line and radial distance from source.

Inverse square effects: for points close to linear source, exposure rate is lower than corresponding point source, but at further distances, it becomes similar to point source rate.

Dose rate at point P with polar coordinates $r$ and $\theta$: $\dot{D}(r,\theta) = \Lambda S_k \frac{G(r,\theta)}{G(1,\pi/2)}F(r,\theta)g(r)$ where $\Lambda$ is the dose rate constant (depends on source, construction, encapsulation), $S_k$ is air kerma strength, $G(r,\theta)$ is the geometry factor (cm^-2) (depends on source distribution and is $1/r^2$ for a point source), $F(r,\theta)$ is anisotropy factor (angular dependence of absorption and scatter), and $g(r)$ is the radial dose function (radial dependence of absorption and scatter).

Isodose curves can be generated with computers. Can use film and TLDs to check computation.

Implant dosimetry

Want to optimize dose distribution. Now typically done with computer algorithms.
Most heavily governed by inverse square law.

Paterson-Parker system: Goal of uniform dose (±10%) to plane or volume using sources of varying strength. Uses dosage tables.
Peripheral radium vs total over area depends on implant size (smaller, more in periphery).
Needles within 1 cm. Uncrossed ends → smaller area of dose uniformity
ETC.

Quimby system: uniform distribution of sources of equal linear activity → nonuniform dose distribution (higher in center)

Memorial system: extension of the Quimby system, lattices of points 1 cm apart.

Paris system: for removable implants of long line sources. Wider spacing for longer sources or larger volumes.

Computer system: sources of uniform strength spaced uniformly (e.g., 1 or 1.5 cm apart) over treatment volume.
It is better to implant a larger volume than to select a lower-value isodose curve to increase the coverage.

Computer dosimetry calculates dose from each seed source and adds. Can use orthogonal x-rays to determine source locations.

Afterloading: Applicators are placed interstitially, on surface, or intra-cavitary. After placement is verified radiographically (and possibly dosimetry), the afterloading machine (or manually in some cases) places the radioactive seeds or wire, or moves a seed to various locations in the applicator to deliver the desired dose to that point.

Low dose rate (LDR) treatments can last several days (hospitalization) with source in place most of the time
Typical sources are ¹²⁵I (T_1/2 = 59 days) and ¹⁰³Pd (T_1/2 = 17 days). Less than 2 Gy/hr.

High dose rate (HDR) treatments usually last several minutes (outpatient), and might be delivered in a few fractions, with sources of high activity (~10 Ci), typically ¹⁹²Ir (T_1/2 = 74 days). Rooms are heavily shielded, as is source in retracted position.
Dose placement is specified by dwell position and dwell time. More than 12 Gy/hr.
Output should be within 5% and source position accuracy within 1 mm (NRC).

Radiation safety and shielding

Level of shielding differs depending on if an area is controlled or uncontrolled.
Maximum permissible dose, P, is 0.1 mSv/wk, and 0.02 mSv/wk & max dose in 1 hour < 0.02 mSv, respectively.

Three types of radiation to protect against: primary (from beam directly), scattered (from machine and patient), leakage (from source housing).

Two types of barrier: Primary (attenuates useful beam) and secondary (attenuates scatter and leakage).

Thickness of barrier depends on the following

Workload (W) - x-rays: mA-min/wk of beam on time. MV: typically dose delivered at 1 m from source. Patients/wk * dose/patient.
- Units of dose/wk at 1 m.
Use factor (U) - Fraction of operating time directed at a particular barrier
- e.g., 0.25 for 90 degrees rotation
Occupancy factor (T) - Fraction of operating time area beyond barrier is occupied by an individual.
- 1 for offices, treatment planning suites, nurses stations, adjacent waiting areas
- 1/2 for adjacent treatment/examination room
- 1/5 corridor, lounges, employee rest rooms
- 1/8 vault doors
- 1/20 public rest rooms, storage, vending, holding area, closets
- 1/40 outdoor areas with pedestrians, parking lots, stairways, elevators
Distance (d) - distance in meters from radiation source to protected area (use 1 foot = 0.3 m from walls)
- Assumes inverse square effects

Transmission factor: $B = \frac{P \cdot d^2}{WUT}$ for primary radiation

Barrier thickness in number of tenth-value-layers: $n = -\text{log}(B)$

Barrier thickness: $t = TVL_1 + (n-1) TVL_e$ where $TVL_1$ is first TVL and $TVL_e$ is equilibrium TVL for a given shielding material. Equilibrium TVL is used to account for beam hardening and low energy scattering in subsequent layers.

Typical materials: concrete, high density concrete, steel, lead. Space and cost considerations.

Scatter transmission factor: $B_s = \frac{P}{\alpha W T} \cdot \frac{400}{F} \cdot d^2 \cdot d'^2$
where $\alpha$ is fractional scatter at 1 m from the scatterer, $d$ is distance from source to scatterer (e.g., patient), $d'$ is distance from scatterer to area, and $F$ is area of beam at scatterer (relative to the standard of 400 cm²). U=1 (all directions).
$\alpha$ depends on angle and beam quality (~0.1% for 90-degrees), tabulated.

Leakage transmission factor $B_l = \frac{P \cdot d^2}{0.001 WT}$ where 0.001 comes from accepting 0.1% leakage from MV machine housing and U=1 (all directions). Roughly same photon quality as primary beam.

Usually leakage barrier exceeds scatter barrier needs (more penetrating radiation) at MV range. Primary radiation barrier covers leakage and scatter.
"Two source rule": For secondary barriers, calculate leakage and scatter thickness separately. If one is more than 1 TVL thicker, use that. If not, add 1 HVL to larger HVL.

Doors must have similar shielding as walls. Can be very heavy. Can use maze instead (multiply scattered radiation at door only, reduced energy and intensity).

Dose at primary barrier:
$D_p = D_{iso} B / d_{pri}^2$ where $D_{iso}$ is dose rate at isocenter, $B$ is transmission factor, and $d_{pri}$ is distance from barrier
Primary barrier for 6/18x linac is usually 170 cm thick concrete (Co-60 teletherapy ~ 70 cm).

Neutrons: Important for ≥ 10 MV beams. Spectrum max around 1 MeV. Concrete from x-ray shielding sufficient for neutrons, but doors require more consideration. Can reduce fluence by 10^-2 through maze. Add hydrogenous material at door to thermalize. Need lead also to stop neutron-capture γ-rays, if maze isn't very long.

Different treatment procedures may have different workloads and use factors (conventional, TBI, IMRT, etc). Need to add up: $\sum{W_i U_i}$ based on actual/expected usage.
TBI may have different distances.
Leakage needs to be modified for IMRT: $C = MU_{imrt} / MU_{conv}$, where $C$ is usually 2 to 10 depending on type. $W = W_{conv} + C\cdot W_{IMRT} + ...$

Shielding brachytherapy sources

Time, distance, shielding.

Lead-lined safes and drawers. L-blocks for source preparation. Lead glass windows for viewing sources, or patients in HDR rooms.

Leak testing of sealed sources (wipe tests). Leaking if 0.005 μCi or more removable contamination is measured.

HDR source housing: allow ≤ 1 mR/hr at 10 m from unit.
Source activity verified to within 2% of specified value. Measured in the well chamber. Less than 10 Ci.
$B = \frac{P \cdot d^2}{WT}$ (U=1 because source is isotropic)
Negligible leakage
$W = \dot{R} \cdot f \cdot t$, where $\dot{R} = A\Gamma / r^2$ is exposure rate based on activity and distance, $t$ is the time the source is out per week, $f = 0.96\, \text{cGy/R}$ is f-factor for ¹⁹²Ir and $f = 0.97\, \text{cGy/R}$ is f-factor for ¹³⁷Cs
HDR ¹⁹²Ir: TVL concrete ~ 20 cm, typically need total of about 50 cm.
LDR ¹³⁷Cs: TVL ~ 2.5 cm lead, typically need 3.0 cm lead.

Surveys

Need sensitive detectors for low levels: ionization chambers, Geiger counters, TLDs, photographic film.

Ionization chamber: large volume (~600 ml), direct-current voltage applied, collects ions created by radiation. Amplified. Current proportional to exposure rate.

Geiger-Müller counters: Cylindrical cathode with fine wire along axis. Pressurized gases. Voltage above saturation applied. Avalanche of charge generated. More sensitive than ionization chamber (can detect individual photons), but less quantitative. Slow recovery time.

Neutron detectors: In beam with activation detectors. Phosphorus: ³¹P(n,p)³¹Si and ³¹P(n,γ)³²P where products emit betas and counted with liquid scintillator. Moderated activation detectors used outside beam (remmeters and foil detectors).
Ion chamber with hydrogenous walls - detects neutrons and x-rays (compare to x-ray only chamber).
Proportional counter, filled with BF₃ for thermalized neutrons: ¹⁰B(n,α)⁷Li

Film to measure leakage from machine head with collimator closed. Ionization chamber at distance of 1 m.

Measure exposure in areas around treatment room with beam pointed in various directions at a phantom.

Regulations

NRC regulated reactor byproducts, accelerator-produced radioactive material, source of radium-226.
10 CFR Part 35
X-ray machines regulated by individual states.
Agreement states can enforce NRC regulations.

Quality Assurance

Control and maintain standard of quality. ACR, ASTRO, AAPM have proposed model QC programs.

Adequate staffing. Communication. Training. Review of QC program.

Dosimetric accuracy

Want ±5% accuracy in dose delivery

Measurements of dose with various settings done on acceptance.
Annual checks.

TG-53: Quality assurance for clinical radiotherapy treatment planning

TG-51 (calibration protocol for photon and electron beams)

TG-21 (1983): calibration protocol for high-energy photon and electron beams using exposure / kerma factors
TG-51 (1999): supercedes TG-21, uses dose to water factors

TG-51 Photons
Absorbed dose to water (Gy) is $D_w^Q = Mk_QN^{^{60}\text{Co}}_{D,w}$ where $M$ is the correct electrometer reading (see above), $k_Q$ is the quality conversion factor from ⁶⁰Co beam to measured beam energies (depends on ion chamber type), and $N^{^{60}\text{Co}}_{D,w}$ is the calibration factor (Gy/C) in reference conditions.

Dose measurements for photons are typically done at a depth in water of 10 cm with a 10 × 10-cm field size and SSD of 100 cm. The quality of a beam can be described by this quantity, "%dd(10)" (k_Q depends on this value, decreases with increased E.)
6 MV: %dd(10) ~ 67
10 MV: %dd(10) ~ 73
For cylindrical or spherical chambers, the measured depth-ionization data should be shifted upstream by 0.6r_cav to give PDD.

· When using an SSD setup, the field size is defined at the surface of the
- D(dmax)=D(dref)/PDD(dref) for SSD setup
· When using an SAD setup, the field size is defined at the detector position which is placed at 10 cm depth at the isocenter of the machine.phantom.
- D(dmax)=D(dref)/TMR(dref) for SAD setup

TG-51 Electrons
Absorbed dose to water (Gy) is $D_w^Q = M k_{Q} N^{^{60}\text{Co}}_{D,w} = MP^Q_{gr}k_{R_{50}}' k_{ecal} N^{^{60}\text{Co}}_{D,w}$ where $M$ is the correct electrometer reading (see above), $P^Q_{gr}$ is a gradient correction factor, $k_{R_{50}}$ is the quality conversion factor, $k_{ecal}$ is the photon-electron conversion factor (depends on ion chamber type), and $N^{^{60}\text{Co}}_{D,w}$ is the calibration factor (Gy/C) in reference conditions.

Dose measurements for electrons are done with ≥10 × 10-cm field size and 100 cm SSD. Depth is relative to the depth in water where the percent depth dose is 50%: $R_{50}$.

Electrons measurement depth: $d_{ref} = 0.6 R_{50} - 0.1 \text{cm}$
$R_{50} = 1.029 I_{50} - 0.06$ where $I_{50}$ is point of 50% ionization

TG-25 (1999) and TG-70 (2009 supplement): electron beam dosimetry

TG-61: 40–300 kV x-ray beam dosimetry

TRS-398: IAEA recommendations for "Absorbed Dose Determination in External Beam Radiotherapy"
Similar to TG-51 and TG-61

TG-119: IMRT Commissioning Tests

TG-142 (partial update of TG-40): Quality assurance of medical accelerators. Includes IMRT/SRS/SBRT

TG-106: Accelerator beam data commissioning equipment and procedures

Regulations: NRC / states
Recommendations: AAPM (TG protocols), ACR and ASTRO (accreditation and guidelines)
NCRP: data/info
RPC: independent verification
QUANTEC: Quantitative Analysis of Normal Tissue Effects in the Clinic

Other tests

CT transfer

DVH and geometry verification

HU to electron density - calibration phantom

Tags: Therapeutic

Previous subject Next subject